Hàn Tín là một vị tướng nhà Hán, Trung Quốc. Ông có cách điểm binh rất tài tình; muốn biết số quân chính xác là bao nhiêu, ông cho lần lượt phất ba lá cờ màu khác nhau, quân lính cứ theo màu cờ quy ước mà lần lượt xếp hàng 3, 5, 7 rồi báo cáo cho ông biết số người thừa. Gọi số người thừa là a, b, c thì số quân bằng 70a + 21b + 15c + bội 105.Muốn cho dễ nhớ ông đặt thành thơ:
"Ba người cùng đội 70 rành
Năm khóm hoa mai, hai mốt cành
Bảy gã vườn đào chơi nửa tháng
Cộng hoặc trừ trăm linh năm tính nhẩm nhanh."
a)Hãy áp dụng công thức Hàn Tín để giải bài toán sau: Số học sinh tham dự giải thưởng Lương Thế Vinh vào khoảng 4600 đến 4700 học sinh, biết rằng xếp hàng 3 dư 2; xếp hàng 5 dư 3 và xếp hàng 7 dư 4. Tính số học sinh tham dự.
b)Giải thích công thức trên của Hàn Tín

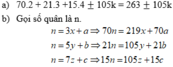
a) Số học sinh tham dự giải Lương Thế Vinh là:
70.2 + 21.3 + 15.4 + 105m \(\left(m\in N\right)\)= 263 + 105m
Theo đầu bài, ta có: \(4600\le263+105m\le4700\)
\(4337\le105m\le4367\)
\(4337>105.41;4367< 105.43\)
Do đó 41 < m < 43 nên m = 42
Vậy số học sinh tham dự giải Lương Thế Vinh là:
263 + 105.42 = 4673 (học sinh)
b) Gọi số quân là x
Ta có: \(x-a⋮3\Rightarrow70x-70\text{a}⋮105\)
\(x-b⋮5\Rightarrow21\text{x}-21b⋮105\)
\(x-c⋮7\Rightarrow15\text{x}-15c⋮105\)
Do đó \(\left(70\text{x}+21\text{x}+15\text{x}\right)-\left(70\text{a}+21b+15c\right)⋮105\)
\(106x-\left(70\text{a}+21b+15c\right)⋮105\)
Vậy \(x=70\text{a}+15b+21c\pm b\text{ội}105\)