Cho tam giác ABC có \(\widehat{B}90^o\). Vẽ đường phân giác AD và đường cao AH của tam giác ABC
a. CMR: \(2\widehat{HAD}=\widehat{HAB}+\widehat{HAC}\)
b. CMR: \(\widehat{ABC}=90^o+\widehat{HAB}\) và \(\widehat{ACB}=90^o-\widehat{HAC}\)
c. CMR:...
Đọc tiếp
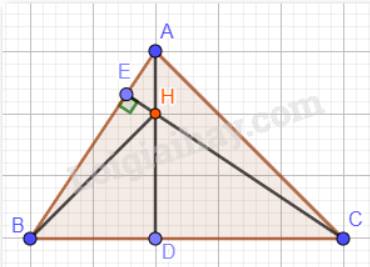
Cho tam giác ABC có \(\widehat{B}>90^o\). Vẽ đường phân giác AD và đường cao AH của tam giác ABC
a. CMR: \(2\widehat{HAD}=\widehat{HAB}+\widehat{HAC}\)
b. CMR: \(\widehat{ABC}=90^o+\widehat{HAB}\) và \(\widehat{ACB}=90^o-\widehat{HAC}\)
c. CMR: \(\widehat{DAH}=\dfrac{1}{2}\left(\widehat{ABC}-\widehat{ACB}\right)\)
b: Vì góc ABC là góc ngoài cua ΔAHB
nên góc ABC=góc AHB+góc HAB=90 độ+góc HAB
Xét ΔHAC vuông tại H có góc HAC+góc ACB=90 độ
=>góc ACB=90 độ-góc HAC
c: 1/2(góc ABC-góc ACB)
=1/2(180 độ-góc ABH-90 độ+góc HAC)
=1/2(90 độ-góc ABH+góc HAC)
=góc DAH