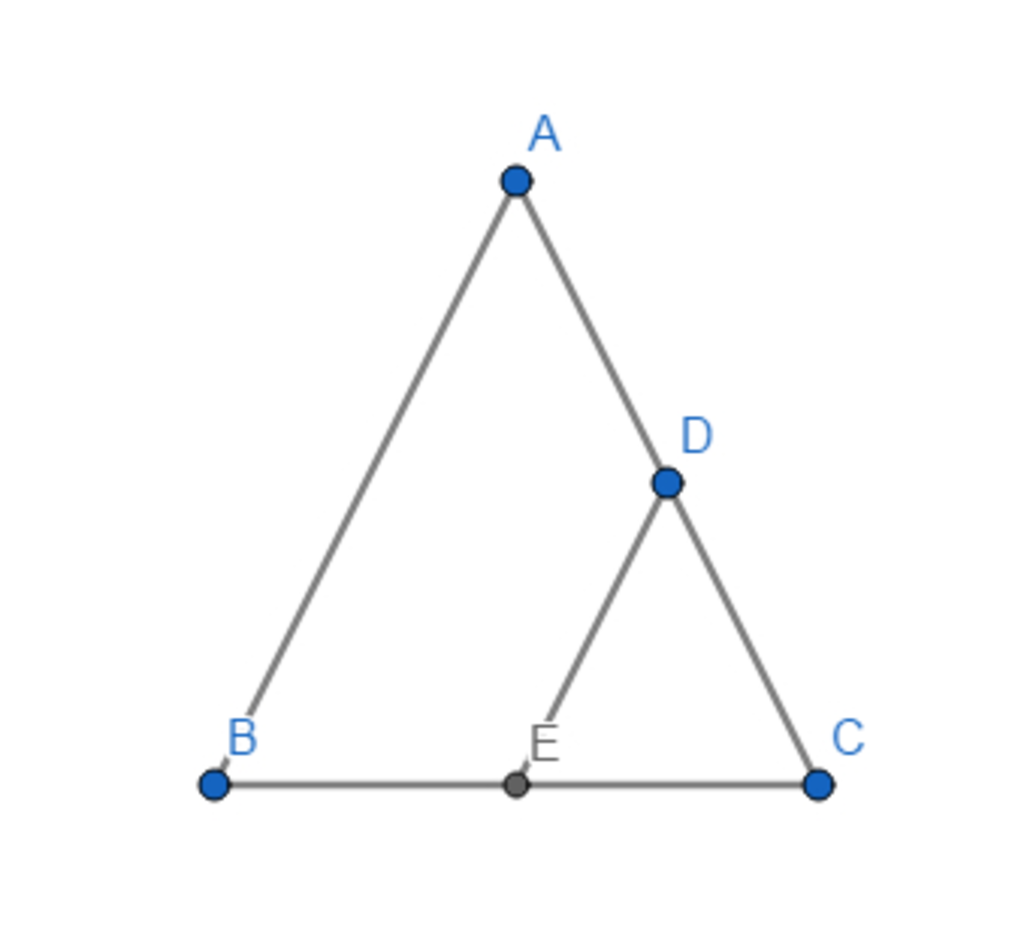
Cho tam giác ABC cân tại A điển O nằm trong tam giác đó trên cạnh AB lấy điểm D . trên cạnh BC lấy điểm E sao cho OD song song BC . OE song song AC .Chứng Minh rằng tứ giác DOEB là hình thang cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài này rất dễ nên mình sẽ giúp bạn
OD song song với BE(gt) nên DOEB là hình thang (1)
OE song song với AC(gt) nên góc OEB = góc C (đồng vị)
Mặt khác, tam giác ABC cân tại A (gt)
Suy ra: góc B = góc C (tính chất tam giác cân)
Do đó: góc B = góc OEB (2)
Từ (1) và (2) suy ra: ODEB là hình thang cân(vì có 2 góc kề 1 đáy bằng nhau)
Chúc bạn học tốt.

a: Xét ΔABM vuông tại M và ΔACM vuông tại M có
AB=AC
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
c: Ta có: AD+DB=AB
AE+EC=AC
mà AD=AE và AB=AC
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
=>\(\widehat{DCB}=\widehat{EBC}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
=>\(\widehat{BAI}=\widehat{CAI}\)
=>AI là phân giác của góc BAC

Ta có:
DE // AB (gt).
=> Góc B = Góc DEC (2 góc ở vị trí đồng vị).
Mà Góc B = Góc C (Tam giác ABC cân tại A).
=> Góc DEC = Góc C.
=> Tam DEC là tam giác cân tại D.
Ta có: \(\widehat{BEO}=\widehat{C}\)
mà \(\widehat{C}=\widehat{B}\)
nên \(\widehat{BEO}=\widehat{B}\)
Xét tứ giác BDOE có OD//BE
nên BDOE là hình thang
mà \(\widehat{BEO}=\widehat{B}\)
nên BDOE là hình thang cân