Tìm a,b để f(x)=x4-3x3+x2+ax chia hết cho g(x)=x2-3x+2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 10 2021
\(f\left(x\right)⋮g\left(x\right)\)
\(\Leftrightarrow x^4-3x^3+4x^2-x^2+3x-4+\left(a-3\right)x+\left(b+4\right)⋮x^2-3x+4\)
\(\Leftrightarrow\left(a,b\right)=\left(3;-4\right)\)
CM
18 tháng 12 2017
Ta có
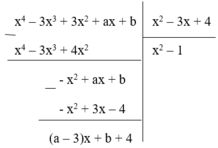
Phần dư của phép chia f(x) cho g(x) là R = (a – 3)x + b + 4. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 3)x + b + 4 = 0, Ɐx ó a - 3 = 0 b + 4 = 0
ó a = 3 b = - 4 => ab = -12
Đáp án cần chọn là: A
Z2
2
CM
21 tháng 10 2017
Ta có
Phần dư của phép chia f(x) cho g(x) là R = (a – 1)x + b + 30
Để phép chia trên là phép chia hết thì R = 0 với mọi x
ó (a – 1)x + b + 30 = 0 với mọi x
ó a - 1 = 0 b + 30 = 0 ó a = 1 b = - 30
Vậy a = 1; b = -30
Đáp án cần chọn là: D
MV
0
14 tháng 11 2022
a: f(x) chiahết cho g(x)
=>\(x^4-x^2-3x^3+3x+\left(b+1\right)x^2-\left(b+1\right)+\left(a-3\right)x+2b+1⋮x^2-1\)
=>a-3=0 và 2b+1=0
=>a=3 và b=-1/2
b: A=2x^2-3x
=2(x^2-3/2x)
=2(x^2-2*x*3/4+9/16-9/16)
=2(x-3/4)^2-9/8>=-9/8
Dấu = xảy ra khi x=3/4
7 tháng 11 2021
a: \(\Leftrightarrow2x^2+8x+\left(a-8\right)x+4\left(a-8\right)-4a+28⋮x+4\)
hay a=7
17 tháng 9 2021
\(1,A⋮B\Leftrightarrow x^3-3x^2-ax+3=\left(x-1\right)\cdot a\left(x\right)\)
Thay \(x=1\)
\(\Leftrightarrow1-3-a+3=0\\ \Leftrightarrow a=1\)
\(2,A⋮B\Leftrightarrow3x^3-16x^2+25x+a=\left(x^2-4x+3\right)\cdot b\left(x\right)\\ \Leftrightarrow3x^3-16x^2+25x+a=\left(x-3\right)\left(x-1\right)\cdot b\left(x\right)\)
Thay \(x=1\)
\(\Leftrightarrow3-16+25+a=0\\ \Leftrightarrow a=-12\)
Thay \(x=3\)
\(\Leftrightarrow3\cdot27-16\cdot9+25\cdot3+a=0\\ \Leftrightarrow81-144+75+a=0\\ \Leftrightarrow12+a=0\Leftrightarrow a=-12\)
Vậy \(a=-12\)
AH
Akai Haruma
Giáo viên
14 tháng 7 2023
Lời giải:
Ta thấy: $x^2-3x+2=(x-1)(x-2)$. Do đó để $f(x)$ chia hết cho $g(x)$ thì $f(x)\vdots x-1$ và $f(x)\vdots x-2$
Tức là $f(1)=f(2)=0$ (theo định lý Bê-du)
$\Leftrightarrow 3-2+(a-1)+3+b=3.2^4-2.2^3+(a-1).2^2+3.2+b=0$
$\Leftrightarrow a+b=-3$ và $4a+b=-34$
$\Rightarrow a=\frac{-31}{3}$ và $b=\frac{22}{3}$
b đâu?