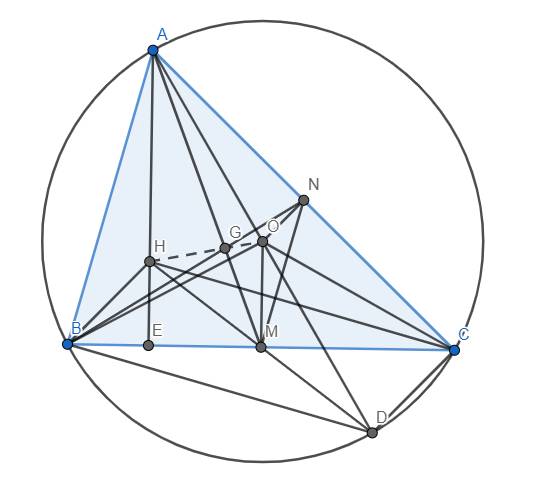
Cho tam giác ABC có 3 góc nhọn, các điểm M,N thứ tự là trung điểm của BC và AC. Các đường trung trực của BC và AC cắt nhau tại O. Qua A kẻ đường thẳng song song với OM, qua B kẻ đường thẳng song song với ON, chúng cắt nhau tại H.
a, Nối MN, Tam giác AHB đồng dạng với tam giác nào?
b. Gọi G là trọng tâm tam giác ABC, chứng minh tam giác AHG đồng dạng với MOG
c. Chứng minh ba điểm H,O,G thẳng hàng.
Giúp mình nhé!! Thanks nhìu