Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Em tham khảo tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
hihihihihihiihiihiihihiihihihihihihihihihihihihihihiihihiihihihihihihiihihihihihihihihihihihihihihihihhihihihihihihihhiihihihihihiihihiihihihihihihihihihihihihihihihihiihihihihihiihihihihihihihihihiihihihihiihiihihihihiihihihihihiihihihihihiihhiihihihiihihihihihiihihihihhiihhiihiihihihihihihihihihihihiihhiiihhiihhiihihihihihihihiihihih
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
=>AM=DE
b: ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
=>I là trung điểm của AM
Gọi H,K lần lượt là trung điểm của AB,AC
Xét ΔABC có
H,K lần lượt là trung điểm của AB,AC
=>HK là đường trung bình
=>HK//BC và HK=BC/2
Xét ΔAMB có
I,H lần lượt là trung điểm của AM,AB
=>IH là đường trung bình
=>IH//MB và IH=MB/2
=>IH//BC
mà KH//BC
nên I,K,H thẳng hàng
=>I di chuyển trên đoạn KH là đường trung bình của ΔABC
Xét tứ giác ADME, ta có:
∠ A = 90 0 (gt)
MD ⊥ AB (gt)
⇒ ∠ (MDA ) = 90 0
ME ⊥ AC (gt)
⇒ ∠ (MEA ) = 90 0
Suy ra tứ giác ADME là hình chữ nhật ( vì có ba góc vuông)
⇒ AM = DE ( tính chất hình chữ nhật)
a) Xét tứ giác AEMF có
\(\widehat{AFM}=90^0\)(gt)
\(\widehat{AEM}=90^0\)(gt)
\(\widehat{FAE}=90^0\)(gt)
Do đó: AFME là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Suy ra: AM=EF(Hai đường chéo của hình chữ nhật AFME)
b) Gọi O là giao điểm của AM và EF
Ta có: AMFE là hình chữ nhật(cmt)
nên Hai đường chéo AM và EF cắt nhau tại trung điểm của mỗi đường và bằng nhau(Định lí hình chữ nhật)
mà O là giao điểm của AM và EF(gt)
nên O là trung điểm của AM; O là trung điểm của EF
Ta có: ΔAHM vuông tại H(gt)
mà HO là đường trung tuyến ứng với cạnh huyền AM(O là trung điểm của AM)
nên \(HO=\dfrac{AM}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà AM=EF(cmt)
nên \(HO=\dfrac{EF}{2}\)
Xét ΔHFE có
HO là đường trung tuyến ứng với cạnh EF(O là trung điểm của EF)
\(HO=\dfrac{EF}{2}\)(cmt)
Do đó: ΔHFE vuông tại H(Định lí 2 về áp dụng hình chữ nhật vào tam giác vuông)
Em tham khảo bài toán tương tự tại link dưới đây nhé:
Câu hỏi của Trần Thị Vân Ngọc - Toán lớp 8 - Học toán với OnlineMath
Chú ý rằng: EF//BC, EF, BC đều cố định nên khoảng cách giữa 2 đường thẳng này là cố định.
Vậy thì I luôn cách BC một khoảng cố định.
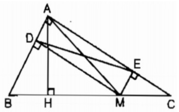
a) Xét tứ giác DMEA có 3 góc vuông nên DMEA là hình chữ nhật.
Theo tính chất hình chữ nhật thì AM = DE.
b) Do DMEA là hình chữ nhật nên DE giao AM tại trung điểm mỗi đường. Do đó, I cũng là trung điểm AM.
Gọi K, H lần lượt là trung điểm của AB và AC.
Xét tam giác BAM có K, I lần lượt là trung điểm của AB và AM nên KI là đường trung bình.
Vậy IK// BC. Tương tự IH//BC.
Lại có KE//BC nên I thuộc KH.
Do KH cố định nên ta có: Khi M di chuyển trên đoạn BC thì I di chuyển trên đoạn KH.
c) Ta đã có DE = AM nên DE ngắn nhất khi và chỉ khi AM có độ dài ngắn nhất.
Lại có AM là đường xiên nên luôn luôn lớn hơn hoặc bằng đường cao AH.
Vậy thì AM có độ dài ngắn nhất khi AM trung với AH tức là M trùng H.
Tóm lại DE có độ dài ngắn nhất khi M là chân đường vuông góc hạ từ A xuống BC.