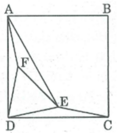
Cho hình vuông ABCD. Vẽ E trong hình vuông sao cho góc EBC = góc ECD((hay góc BCD gì đó. xin lỗi chỗ này không nhớ rõ lắm, mn thấy cái nào làm đc thì cứ lấy cái góc đó) = 150.
a. Vẽ F trong hình vuông sao cho góc FAB = góc FDA = 150. CMR: tam giác ECD là tam giác đều.
b. CMR: tam giác ABE là tam giác đều.