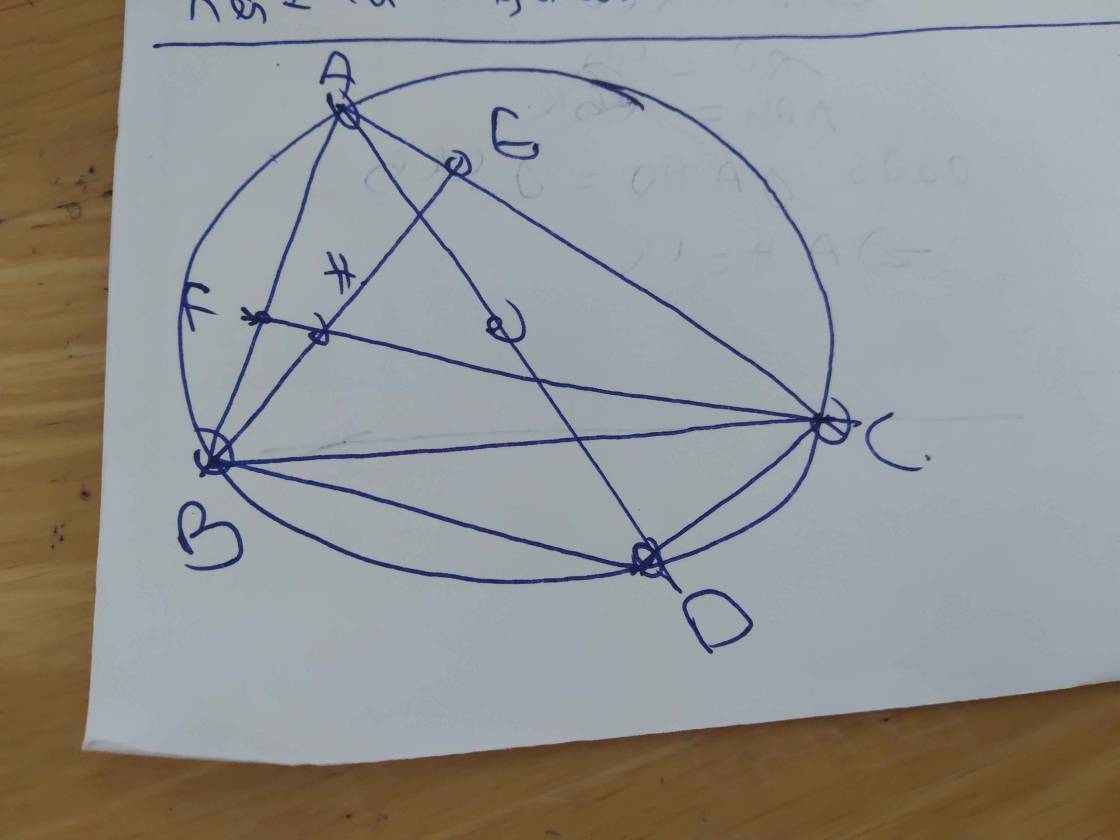
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O, các đường cao BE, CF cắt nhau tại H
a) Chứng minh rằng: 4 điểm B, F, E, C thuộc cùng một đường cao
b) Kẻ đường kính AA' của đường tròn tâm O. Chứng minh: tứ giác BHCA' là hình bình hành
c) Chứng minh: 4 điểm A, F, H, E cùng thuộc một đường tròn