Câu 5. Cùng một lúc tại hai điểm A và B cách nhau 10 km có hai ô tô chạy cùng chiều thẳng đều từ A đến B. Vận tốc của ô tô tại A là 54 km/h và của ô tô từ B là 48 km/h. Chọn A làm gốc tọa độ, thời điểm xuất phát của hai xe làm mốc thời gian và chiều chuyển động của hai xe ô tô là chiều dương. a. Viết phương trình chuyển động của hai xe ô tô trên. b. Xác định thời điểm và vị trí hai xe gặp nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn gốc tọa độ O trùng A
Chiều dương trục Ox : từ A đến B
a,Phương trình chuyển động của mỗi vật:
\(x_1=72t(km,h)\)
\(x_2=10+54t(km,h)\)
b,Khi 2 xe gặp nhau
\(x_1=x_2 \Rightarrow 72t= 10+54t\Rightarrow t= \dfrac{5}{9} (h)\)
Vậy thời gian 2 xe gặp nhau là sau\(\dfrac{5}{9}\left(h\right)\)
Vị trí gặp cách A :\(72\cdot\dfrac{5}{9}=40\left(km\right)\)
c, < Bạn tự vẽ>

Chọn D
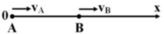
Cách 1:
Từ
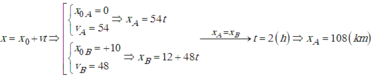
Cách 2:
Mỗi giờ xe A đi được nhiều hơn xe B là 54 – 48 = 6km.
Muốn xe A đi được nhiều hơn xe B là 12 km thì phải cần thời gian: 12/6 = 2h. Lúc này, xe A đi được: AC = 54.2 = 108 km.

Chọn đáp án A
? Lời giải:
− Phương trình chuyển động của xe A: xA = x0A + vAt = 54t (km).
− Phương trình chuyển động của xe B: xB = x0B + vBt = 10 + 48t (km).


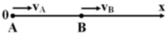



Chọn gốc tọa độ O trùng A
Chiều dương trục Ox : từ A đến B
a,Phương trình chuyển động của mỗi vật:
\(x_1=54t(km,h)\)
\(x_2=10+48t(km,h)\)
b,Khi 2 xe gặp nhau
\(x_1=x_2 \Rightarrow 54t=10+48t\Rightarrow t= \dfrac{5}{3} (h)\)
Vậy thời điểm 2 xe gặp nhau là sau thời điểm xuất phát \(\dfrac{5}{3}\left(h\right)=1h40'\)
Vị trí gặp cách A :54.\(\dfrac{5}{3}=90\left(km\right)\)