Tìm x để \(A=\dfrac{x-\sqrt{4}x+5}{\sqrt{x}-2}\) với x > 2 đạt giá trị nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 10 2021
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)
Ta có: \(P=\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{2}{\sqrt{x}-2}-\dfrac{4\sqrt{x}}{x-4}\)
\(=\dfrac{x-2\sqrt{x}+2\sqrt{x}+4-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
8 tháng 4 2021
a, Ta có : \(x=4\Rightarrow\sqrt{x}=2\)
\(\Rightarrow A=\frac{2+1}{2+2}=\frac{3}{4}\)
Vậy với x = 4 thì A = 3/4
b, \(B=\frac{3}{\sqrt{x}-1}-\frac{\sqrt{x}+5}{x-1}=\frac{3\left(\sqrt{x}+1\right)-\sqrt{x}-5}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\frac{3\sqrt{x}+3-\sqrt{x}-5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\frac{2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\frac{2}{\sqrt{x}+1}\)( đpcm )
NM
1
22 tháng 5 2022
\(A=\sqrt{x}+\dfrac{2}{\sqrt{x}}\ge2\cdot\sqrt{\sqrt{x}\cdot\dfrac{2}{\sqrt{x}}}=2\sqrt{2}\)
Dấu '=' xảy ra khi \(\sqrt{x}\cdot\sqrt{x}=2\)
hay \(x=2\)
LD
17 tháng 5 2021
1. \(x=\frac{1}{9}\) thỏa mãn đk: \(x\ge0;x\ne9\)
Thay \(x=\frac{1}{9}\) vào A ta có:
\(A=\frac{\sqrt{\frac{1}{9}}+1}{\sqrt{\frac{1}{9}}-3}=-\frac{1}{2}\)
2. \(B=...\)
\(B=\frac{3\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\frac{4x+6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\frac{3x-9\sqrt{x}+x+3\sqrt{x}-4x-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\frac{-6\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
3. \(P=A:B=\frac{\sqrt{x}+1}{\sqrt{x}-3}:\frac{-6\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\frac{\sqrt{x}+3}{-6}\)
Vì \(\sqrt{x}+3\ge3\forall x\)\(\Rightarrow\frac{\sqrt{x}+3}{-6}\le\frac{3}{-6}=-\frac{1}{2}\)
hay \(P\le-\frac{1}{2}\)
Dấu "=" xảy ra <=> x=0
AH
Akai Haruma
Giáo viên
10 tháng 8 2021
Bài 5:
\(C=\frac{2\sqrt{x}-3}{\sqrt{x}-2}=\frac{2(\sqrt{x}-2)+1}{\sqrt{x}-2}=2+\frac{1}{\sqrt{x}-2}\)
Để $C$ nguyên nhỏ nhất thì $\frac{1}{\sqrt{x}-2}$ là số nguyên nhỏ nhất.
$\Rightarrow \sqrt{x}-2$ là ước nguyên âm lớn nhất
$\Rightarrow \sqrt{x}-2=-1$
$\Leftrightarrow x=1$ (thỏa mãn đkxđ)
AH
Akai Haruma
Giáo viên
10 tháng 8 2021
Bài 6:
$D(\sqrt{x}+1)=x-3$
$D^2(x+2\sqrt{x}+1)=(x-3)^2$
$2D^2\sqrt{x}=(x-3)^2-D^2(x+1)$ nguyên
Với $x$ nguyên ta suy ra $\Rightarrow D=0$ hoặc $\sqrt{x}$ nguyên
Với $D=0\Leftrightarrow x=3$ (tm)
Với $\sqrt{x}$ nguyên:
$D=\frac{(x-1)-2}{\sqrt{x}+1}=\sqrt{x}-1-\frac{2}{\sqrt{x}+1}$
$D$ nguyên khi $\sqrt{x}+1$ là ước của $2$
$\Rightarrow \sqrt{x}+1\in\left\{1;2\right\}$
$\Leftrightarrow x=0; 1$
Vì $x\neq 1$ nên $x=0$.
Vậy $x=0; 3$
AH
Akai Haruma
Giáo viên
5 tháng 2
Lời giải:
ĐKXĐ: $x\geq 0; x\neq 9$
\(P=2A:B=\frac{2(\sqrt{x}+1)}{x-9}: \frac{2}{\sqrt{x}-3}=\frac{2(\sqrt{x}+1)}{(\sqrt{x}-3)(\sqrt{x}+3)}.\frac{\sqrt{x}-3}{2}=\frac{\sqrt{x}+1}{\sqrt{x}+3}\)
\(P=1-\frac{2}{\sqrt{x}+3}\)
Để $P$ nhỏ nhất thì $\frac{2}{\sqrt{x}+3}$ lớn nhất
$\Leftrightarrow \sqrt{x}+3$ nhỏ nhất
Với $x$ nguyên dương, $\sqrt{x}+3$ nhỏ nhất bằng $\sqrt{1}+3=4$ khi $x=1$
$\Rightarrow P_{\min}=\frac{\sqrt{x}+1}{\sqrt{x}+3}=\frac{1+1}{1+3}=\frac{1}{2}$
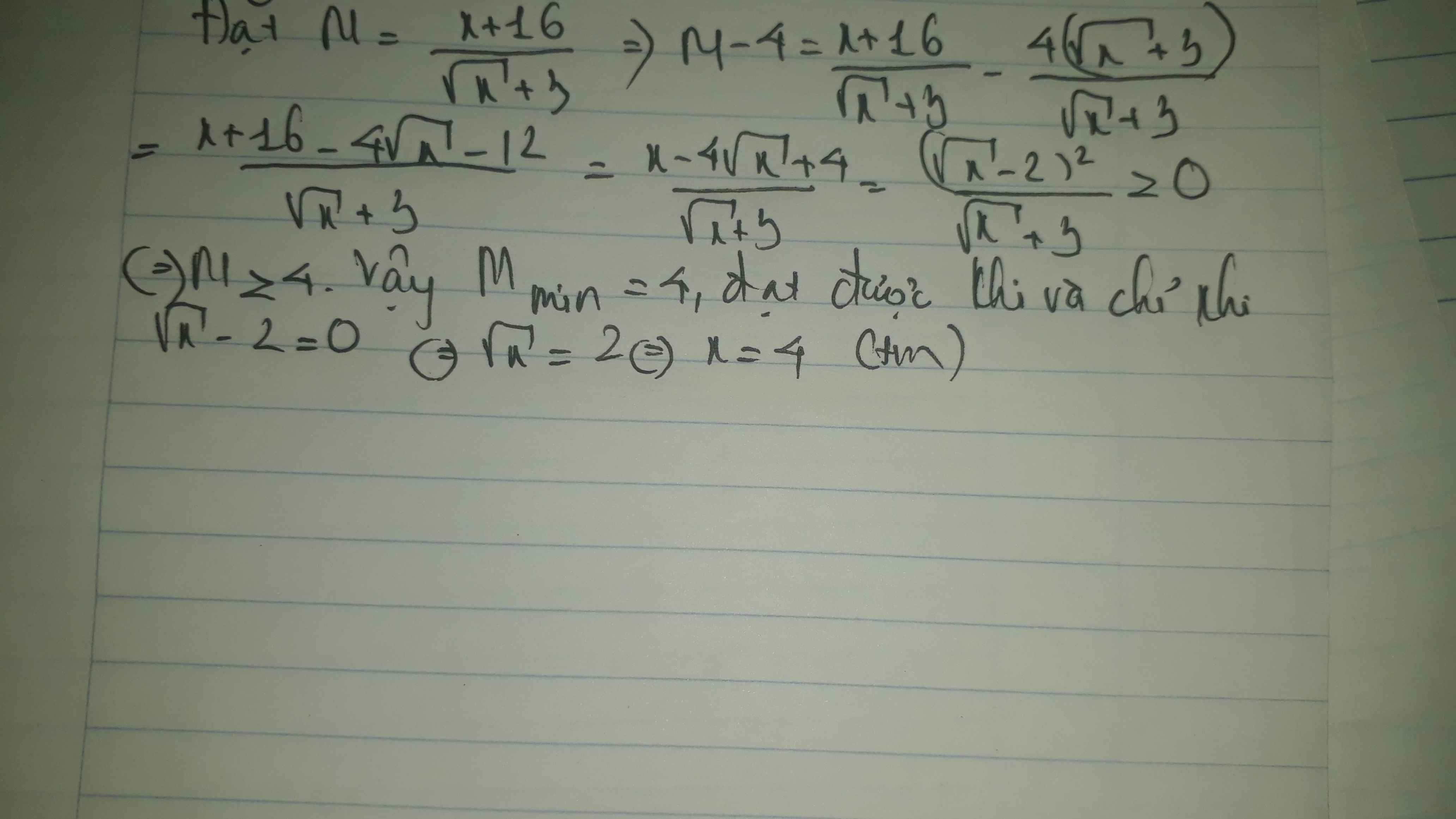
\(A=\dfrac{\left(\sqrt{x}-2\right)^2+1}{\sqrt{x}-2}=\sqrt{x}-2+\dfrac{1}{\sqrt{x}-2}\\ \ge2\sqrt{\left(\sqrt{x}-2\right)\left(\dfrac{1}{\sqrt{x}-2}\right)}=2\cdot1=2\left(BĐT.cauchy\right)\)
Dấu \("="\Leftrightarrow\left(\sqrt{x}-2\right)^2=1\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\)
\(A=\dfrac{x-4\sqrt{x}+5}{\sqrt{x}-2}=\dfrac{\left(\sqrt{x}-2\right)^2+1}{\sqrt{x}-2}=\sqrt{x}-2+\dfrac{1}{\sqrt{x}-2}\)
Áp dụng bất đẳng thức Cauchy cho 2 số dương:
\(A=\sqrt{x}-2+\dfrac{1}{\sqrt{x}-2}\ge2\sqrt{\dfrac{\sqrt{x}-2}{\sqrt{x}-2}}=2\)
\(minA=2\Leftrightarrow\sqrt{x}-2=1\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\)