Giúp mình câu c,d
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)

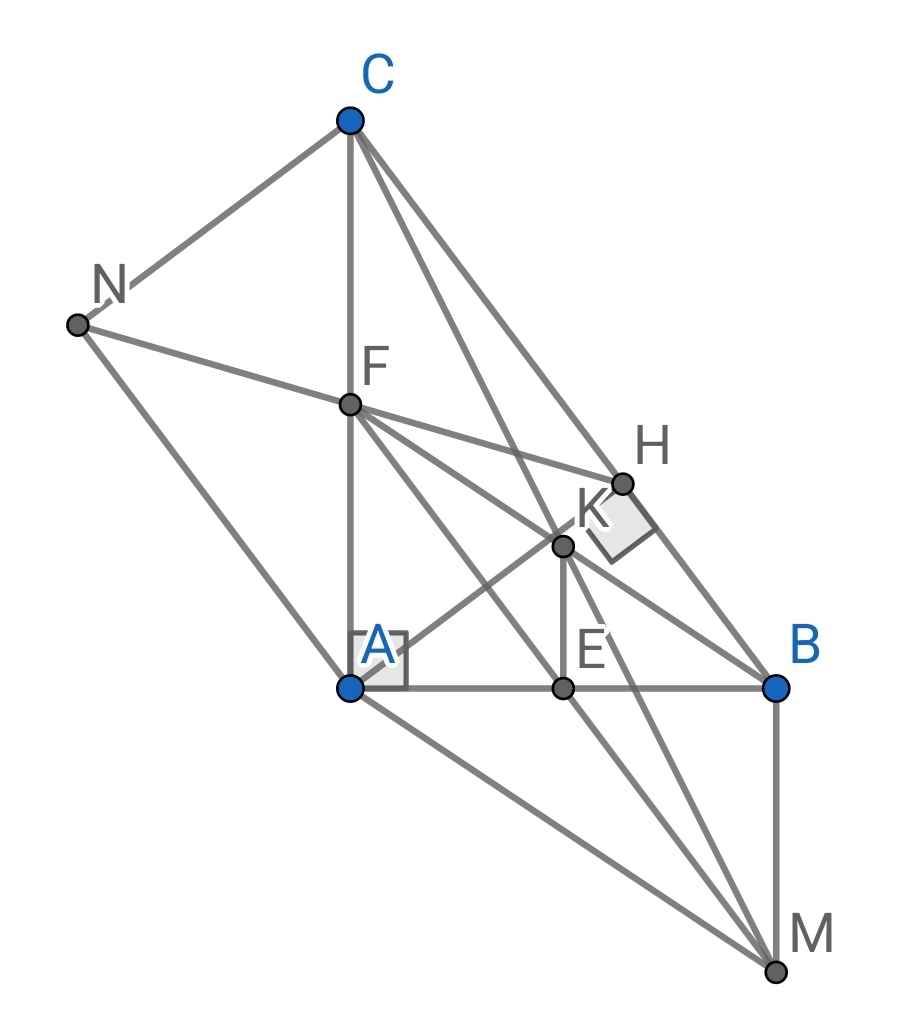 c) Do AMBF là hình bình hành (cmt)
c) Do AMBF là hình bình hành (cmt)
⇒ BM // AF
Mà AF ⊥ AB
⇒ BM ⊥ AB
⇒ ∠ABM = 90⁰
Do AHCN là hình chữ nhật (cmt)
⇒ ∆AHC vuông tại H
F là trung điểm của AC (gt)
⇒ HF = AF = CF = AC : 2
⇒ ∆AHF cân tại F
⇒ ∠AHF = ∠FAH
Mà ∠FAH + ∠HAB = 90⁰
⇒ ∠AHF + ∠HAB = 90⁰
Lại có:
∆AHB vuông tại H
⇒ ∠HAB + ∠HBA = 90⁰
Mà ∠HAB + ∠AHF = 90⁰ (cmt)
⇒ ∠AHF = ∠HBA (1)
Do ∠FHB = ∠AHF + ∠AHB
= ∠AHF + 90⁰ (2)
∠MBH = ∠HBA + ∠ABM
= HBA + 90⁰ (3)
Từ (1), (2), (3) ⇒ ∠FHB = ∠MBH
∆ABC có:
E là trung điểm của AB (gt)
F là trung điểm của AC (gt)
⇒ EF // BC
⇒ FM // BH
Tứ giác BMFH có:
FM // BH (cmt)
⇒ BMFH là hình thang
Mà ∠FHB = ∠MBH (cmt)
⇒ BMFH là hình thang cân
d)
Do AMBF là hình bình hành (cmt)
⇒ AF = BM và AF // BM
Do F là trung điểm của AC (gt)
⇒ AF = CF = AC : 2
⇒ AC = 2AF
Mà AF = BM (cmt)
⇒ CF = BM
Do AF // BM (cmt)
⇒ CF // BM
Tứ giác BCFM có:
CF // BM (cmt)
CF = BM (cmt)
⇒ BCFM là hình bình hành
Mà K là giao điểm của BF và CM (gt)
⇒ K là trung điểm của BF
∆FBM có:
K là trung điểm của BF (cmt)
E là trung điểm của FM (gt)
⇒ EK là đường trung bình của BM
⇒ EK = BM : 2
⇒ BM = 2EK
Do AHCN là hình chữ nhật (cmt)
⇒ AC = HN
Lại có AC = 2AF (cmt)
⇒ HN = 2AF
Mà AF = BM
⇒ HN = 2BM
Mà BM = 2EK
⇒ HN = 2.2EK = 4EK
Vậy HN = 4EK

\(a,\left\{{}\begin{matrix}AB=AC\left(\Delta ABC.cân.tại.A\right)\\\widehat{ABC}=\widehat{ACB}\left(\Delta ABC.cân.tại.A\right)\\AD.chung\end{matrix}\right.\Rightarrow\Delta ADB=\Delta ADC\left(ch-gn\right)\)
\(b,\)Áp dụng định lí Py-ta-go cho tam giác ABD vuông tại D
\(AD^2=AB^2-BD^2=36\\ \Rightarrow AD=6\left(cm\right)\)
\(c,\) Vì tam giác BAC cân tại A nên đường cao AD cũng là trung tuyến
Mà G là trọng tâm nên \(AG=\dfrac{2}{3}AD=\dfrac{2}{3}\cdot6=4\left(cm\right)\)

a.
\(O=AC\cap BD\Rightarrow O\in BD\in\left(SBD\right)\) \(\Rightarrow SO\in\left(SBD\right)\)
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\\AC\perp BD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SBD\right)\Rightarrow AC\perp SD\)
b.
O là trung điểm AC, H là trung điểm AB \(\Rightarrow\) OH là đường trung bình tam giác ABC
\(\Rightarrow OH||BC\Rightarrow OH\perp AB\Rightarrow OH\perp CD\) (1)
Mà \(SO\perp\left(ABCD\right)\Rightarrow SO\perp CD\) (2)
(1);(2) \(\Rightarrow CD\perp\left(SHO\right)\)
c.
Theo cmt trên \(OH||BC\Rightarrow OH||AD\)
\(\Rightarrow\widehat{\left(OH;SD\right)}=\widehat{\left(AD;SD\right)}=\widehat{SDA}\)
\(AC=2a\sqrt{2}\Rightarrow OA=a\sqrt{2}\Rightarrow SA=SB=SC=SD=\sqrt{SO^2+OA^2}=a\sqrt{3}\)
Áp dụng định lý hàm cosin trong tam giác SAD:
\(cos\widehat{SDA}=\dfrac{SD^2+AD^2-SA^2}{2SD.AD}=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\widehat{SDA}=...\)

`@` `\text {Ans}`
`\downarrow`
`c)`
\(2-3^{x-1}-7=11\)
`\Rightarrow`\(3^{x-1}-5=11\)
`\Rightarrow`\(3^{x-1}=11+5\)
`\Rightarrow`\(3^{x-1}=16\)
Bạn xem lại đề
`d)`
\(\left(x-\dfrac{3}{5}\right)\div\dfrac{-1}{3}=-0,4\)
`\Rightarrow`\(x-\dfrac{3}{5}=-0,4\cdot\left(-\dfrac{1}{3}\right)\)
`\Rightarrow`\(x-\dfrac{3}{5}=\dfrac{2}{15}\)
`\Rightarrow`\(x=\dfrac{2}{15}+\dfrac{3}{5}\)
`\Rightarrow`\(x=\dfrac{11}{15}\)
Vậy, \(x=\dfrac{11}{15}\)

b. Ta có ∠GHE=360°-(90°+70°+60°)=140°
mà ∠GHE+x=180°⇒x=180°-140°=40°
c. Ta có 2x=360°-(65°+95°)=200°⇒x=200°:2=100°
d. Ta có ∠LKJ=180°-120°=60°
⇒x=360°-(95°+120°+60°)=85°
 mình xin lỗi vì ảnh kia bị lỗi. Giúp mình câu a,b,c,d nha còn biểu đồ mình đã làm câu 1.4 và 2.4 r nên mn giúp mình các câu còn lại nhé. Cám ơn
mình xin lỗi vì ảnh kia bị lỗi. Giúp mình câu a,b,c,d nha còn biểu đồ mình đã làm câu 1.4 và 2.4 r nên mn giúp mình các câu còn lại nhé. Cám ơn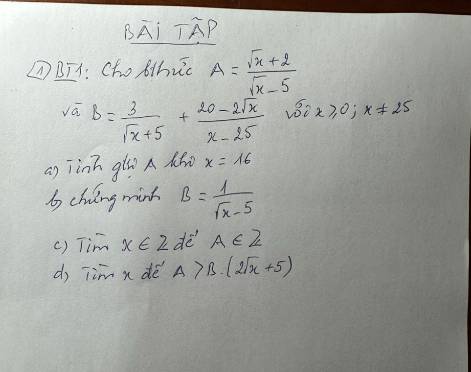



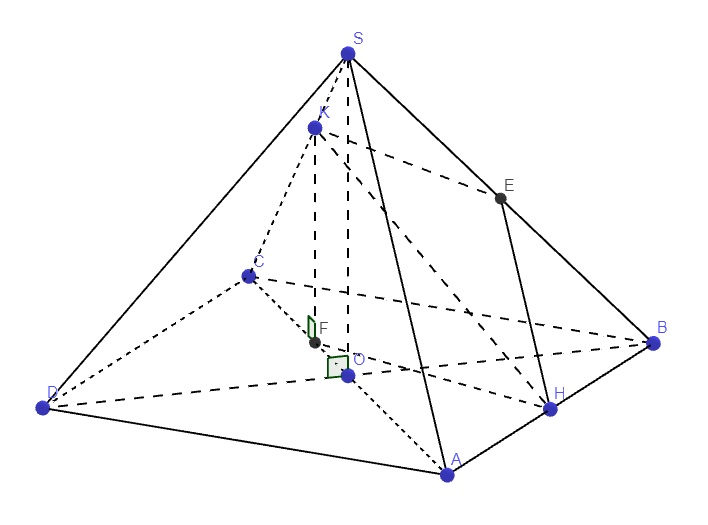
 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 
