Một ô tô xuất phát từ A đến B. Trên nửa quãng đường đầu ô tô đi với vận tốc v1, trên nửa quãng đg sau đi với vận tốc v2. Một ô tô thứ 2 xuất phát từ B đến A, trong nửa thời gian đầu đi với vận tốc v1 và trong nửa t/g sau đi với vận tốc v2. Biết v1=20km/h, v2=60km/h. Nếu xe đi từ B xuất phát muộn hơn 30 phút so với xe đi từ A thì 2 xe đến đích cùng lúc. Tính chiều dài quãng đg AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thời gian đi của ô tô thứ nhất:
\(t_1=\dfrac{s}{2v_1}+\dfrac{s}{2v_2}=\dfrac{s\left(v_1+v_2\right)}{2v_1v_2}\)
Vận tốc trung bình của ô tô thứ nhất:
\(v_{tbA}=\dfrac{s}{t}=\dfrac{2v_1v_2}{v_1+v_2}=\dfrac{2.20.60}{20+60}=30km/h\)
Theo đề ta có: \(s=\dfrac{t_2}{2}v_1+\dfrac{t_2}{2}v_2=t_2\left(\dfrac{v_1+v_2}{2}\right)\)
Vận tốc trung bình của ô tô thứ hai:
\(v_{tbB}=\dfrac{s}{t_2}=\dfrac{v_1+v_2}{2}=\dfrac{20+60}{2}=40km/h\)
Theo đề bài ta có: \(\dfrac{s}{v_A}-\dfrac{s}{v_B}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{s}{30}-\dfrac{s}{40}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{4s}{120}-\dfrac{3s}{120}=\dfrac{60}{120}\)
\(\Leftrightarrow s=60\left(km\right)\)
Vậy hai xe xuất phát cùng lúc sẽ gặp nhau sau:
\(s_1+s_2=s_{AB}\)
\(\Leftrightarrow30t+40t=60\)
\(\Leftrightarrow70t=60\)
\(\Leftrightarrow t=\dfrac{60}{70}\approx0,9\left(h\right)\)
Hai xe gặp nhau tại điểm cách điểm A:
\(s_1=v_A.t=30.0,9=27\left(km\right)\)

Thời gian xe A chạy trên nữa quãng đường đầu:
\(t_1=\dfrac{\dfrac{s_{AB}}{2}}{\upsilon_1}=\dfrac{\dfrac{s_{AB}}{2}}{20}=\dfrac{s_{AB}}{2.20}=\dfrac{s_{AB}}{40}\left(h\right)\)
Thời gian xe A chạy trên nữa quãng đường sau:
\(t_2=\dfrac{\dfrac{s_{AB}}{2}}{\upsilon_2}=\dfrac{\dfrac{s_{AB}}{s}}{60}=\dfrac{s_{AB}}{2.60}=\dfrac{s_{AB}}{120}\left(h\right)\)
Vận tốc trung bình của xe A trên cả quãng đường AB:
\(\upsilon_{tbA}=\dfrac{\dfrac{s_{AB}}{2}+\dfrac{s_{AB}}{2}}{\dfrac{s_{AB}}{40}+\dfrac{s_{AB}}{120}}=\dfrac{s_{AB}}{\dfrac{s_{AB}}{40}+\dfrac{s_{AB}}{120}}=\dfrac{s_{AB}}{\dfrac{s_{AB}}{30}}=30\left(km/h\right)\)
Quãng đường mà xe B đi được trong nữa thời gian đầu:
\(s_1=\upsilon_1.\dfrac{t}{2}=20.\dfrac{t}{2}=10t\left(km\right)\)
Quãng đường xe B đi được trong nữa thời gian sau:
\(s_2=\upsilon_2.\dfrac{t}{2}=60.\dfrac{t}{2}=30t\left(km\right)\)
Vận tốc trung bình của xe B trên cả quãng đường AB:
\(\upsilon_{tbB}=\dfrac{s_1+s_2}{\dfrac{t}{2}+\dfrac{t}{2}}=\dfrac{10t+30t}{t}=\dfrac{40t}{t}=40\left(km/h\right)\)

*đối với người đi từ M đến N
thời gian người đó đi hết nửa quãng đường đầu là
T1=0.5S/v1 =S/40 (h)
thời gian người đó đi hết nửa quãng đường còn lại là
T2=0.5S/V2=S/120 (h)
*Đối với người đi từ N đến M
quãng đường người đó đi được trong nửa giờ đầu là
S1'=0.5t'.v1=10t'(km)
Quãng đường người đó đi trong nửa giờ au là
S2'= 0.5t'.v2=30t'
Mà S1'+S2'=S
10t'+30t'=S
t'=S/40(h)
Vì nếu xe xuất phát từ N đi muộn hơn xe đi từ M 0.5h thì hai xe gặp nhau cùng một lúc nên ta có
T1+T2 =t'+0.5
S/40+s/120=s/40+0.5
S=60(km )

Giải thích các bước giải:
*đối với người đi từ M đến N
thời gian người đó đi hết nửa quãng đường đầu là
T1=0.5S/v1 =S/40 (h)
thời gian người đó đi hết nửa quãng đường còn lại là
T2=0.5S/V2=S/120 (h)
*Đối với người đi từ N đến M
quãng đường người đó đi được trong nửa giờ đầu là
S1'=0.5t'.v1=10t'(km)
Quãng đường người đó đi trong nửa giờ au là
S2'= 0.5t'.v2=30t'
Mà S1'+S2'=S
10t'+30t'=S
t'=S/40(h)
Vì nếu xe xuất phát từ N đi muộn hơn xe đi từ M 0.5h thì hai xe gặp nhau cùng một lúc nên ta có
T1+T2 =t'+0.5
S/40+s/120=s/40+0.5
S=60(km )

mink có câu trả lời rùi
có ai có nhu cầu cần trả lời thì nói mink nha

a) Ta có: \(\left\{{}\begin{matrix}t_1=\dfrac{S_1}{v_1}=\dfrac{S}{2v_1}=\dfrac{S}{40}\left(h\right)\\t_2=\dfrac{S_2}{v_2}=\dfrac{S}{2v_2}=\dfrac{S}{120}\left(h\right)\end{matrix}\right.\)
Vận tốc TB ô tô đi từ M đến N:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{120}}=\dfrac{S}{S\left(\dfrac{1}{40}+\dfrac{1}{120}\right)}=30\left(\dfrac{km}{h}\right)\)
b) Ta có: \(\left\{{}\begin{matrix}S_1'=t_1'.v_1=20t\left(km\right)\\S_2'=t_2'.v_2=60t\left(km\right)\end{matrix}\right.\)
Vận tốc TB ô tô đi từ N về M:
\(v_{tb}'=\dfrac{S_1'+S_2'}{t_1'+t_2'}=\dfrac{20t+60t}{2t}=40\left(\dfrac{km}{h}\right)\)
Thời gian đi và thời gian về lần lượt là:
\(t=\dfrac{S}{30}\left(h\right),t'=\dfrac{S}{40}\left(h\right)\Rightarrow t>t'\)
Vậy thời gian đi nhiều hơn thời gian về
d) Theo đề bài ta có:
\(t-t'=0,5\Rightarrow\dfrac{S}{30}-\dfrac{S}{40}=0,5\Rightarrow S\left(\dfrac{1}{30}-\dfrac{1}{40}\right)=0,5\Rightarrow S_{MN}=60\left(km\right)\)

1/ gọi t1 là thời gian ô tô chạy 1/3 quãng đường đầu
=> t1 = s / ( 3 * v1 ) = s / 120
gọi t2 là thời gian ô tô chạy 1/3 quãng đường tiếp theo
=> t2 = s / ( 3 * v2 ) = s / 150
gọi t3 là thời gian ô tô chạy 1/3 quãng đường cuối cùng
=> t3 = s / ( 3 * v3 )
ta có v tb = s / t = s / ( s / 120 + s / 150 + s / ( 3 *v3) )
=> 45 = s / [s ( 1/ 120 + 1/ 150 + 1/ ( 3 *v3 ) ) ]
=> 45 = 1 / ( 3 / 200 + 1 / ( 3 * v3 )
=> 1 / 45 = 3 / 200 + 1/ ( 3 * v3 )
=> 1 / ( 3 *v3 ) = 1 / 45 - 3 / 200
=> 1 / ( 3 *v3 ) = 13 / 1800
=> 3 * v3 = 1800 / 13
=> v3 = 1800 / 39 = khoảng 46,15 km / h
2/Tính vận tốc trung bình của xe đi từ A đến B
vtb = s/t
theo bài ra ta có : s/2 = 20*t1 và s/2 = 60*t2
=> vtb = s/( t1 + t2) = s/ ( s/40 + s/ 120 ) = 30 (km/h)
Tính vận tốc trung bình của xe đi từ B đến A
theo bài ra ta cũng có
t/2 = s1/20 và t/2 = s2/60
=> vtb" = (s1 + s2 )/t = ( 10t + 30t )/t = 40 ( km/h)
Mà nếu xe từ B xuất phát muộn hơn so với xe xuất phát từ A 30phút = 1/2 h thì 2 xe đến địa điểm cùng 1 lúc
=> sA-B = 30*t
sB-A = 40 * ( t - 1/2)
Mà sA-B = sB-A => 30*t = 40 * ( t - 1/2) => t= 2 (h)
Vậy s = 60 ( km)

a, Thời gian đi xe máy từ A là
\(t=t_1+t_2=\dfrac{s_1}{v_1}+\dfrac{s_2}{v_2}=\dfrac{AB}{2v_1}=\dfrac{AB}{2v_2}=\dfrac{AB}{30}\)
Thời gian xe ô tô đi từ B:
\(AB=v_1.\dfrac{t}{2}+v_2.\dfrac{t}{2}=t\left(\dfrac{v_1}{2}+\dfrac{v_2}{2}\right)=40t\\ \Rightarrow30t_{xe.máy}=49t_{xe.ô.tô}\\ \Rightarrow t_{xm}=\dfrac{4}{3}t_{xôt}\)
Mà
\(t_{xm}=t_{xôt}+0,5\left(30'=0,5h\right)\\ \Rightarrow\left\{{}\begin{matrix}t_{xôt}=1,5\left(h\right)\\t_{xm}=2\left(h\right)\end{matrix}\right.\\ \Rightarrow AB=60km\\ \Rightarrow\left\{{}\begin{matrix}v_{xm}=30\left(km/h\right)\\v_{xôt}=40\left(kmh/\right)\end{matrix}\right.\)
b, Xét thời gian 2 xe đổi \(v\)
\(t_{xôt}=\dfrac{t_{xm}}{2}=0,75\left(h\right)\\ t_{xm}=\dfrac{AB}{2v_1}=1,5\left(h\right)\)
Xe ô tô đổi vận tốc trước :
\(t=0,75\left(h\right)\)
2 xe còn cách nhau :
\(=69-2v_1.0,75=30\left(km\right)\)
Từ t = 0,75(h)
\(\rightarrow Xe.ô.tô.đi.với.v_2,xe.máy.vẫn.v_1\)
2 xe gặp nhau sau :
\(t=\dfrac{30}{\left(v_1+v_2\right)}=0,5\left(h\right)\)
Xe máy đi thêm được \(0,5.v_1=10\left(km\right)\)
Điểm gặp nhau cách A số km là
\(15+10=25\left(km\right)\)

đối với ô tô 1:
\(t_1=\frac{S_1}{v_1}=\frac{S}{2v_1}\)
\(t_2=\frac{S_2}{v_2}=\frac{S}{2v_2}\)
vận tốc trung bình ô tô 1 là:
\(v_{tb1}=\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{2v_1}+\frac{S}{2v_2}}=\frac{1}{\frac{1}{2v_1}+\frac{1}{2v_2}}=\frac{2v_1v_2}{v_1+v_2}\)
đối với ô tô thứ hai :
\(S_1=v_1t_1=\frac{v_1t}{2}\)
\(S_2=v_2t_2=\frac{v_2t}{2}\)
vận tốc trung bình của ô tô hai là:
\(v_{tb2}=\frac{S_1+S_2}{t}=\frac{\frac{v_1t+v_2t}{2}}{t}=\frac{v_1+v_2}{2}\)
ta lấy vận tốc trung bình của ô tô 1 trừ cho của ô tô 2 thì:
\(\frac{2v_1v_2}{v_1+v_2}-\frac{v_1+v_2}{2}=\frac{4v_1v_2-\left(v_1+v_2\right)^2}{2\left(v_1+v_2\right)}\)
\(=\frac{4v_1v_2-v_1^2-2v_1v_2-v_2^2}{2\left(v_1+v_2\right)}=\frac{-\left(v_1-v_2\right)^2}{2\left(v_1+v_2\right)}\)
do (v1-v2)2 luôn luôn lớn hơn hoặc bằng 0 nên:
-(v1-v2)2<0
từ đó ta suy ra vận tốc trung bình của ô tô 1 bé hơn vận tốc trung bình của ô tô 2 nên ô tô 2 đến trước
(do bạn không cho biết v1 và v2 nên mình không biết tính thời gian ra sao)
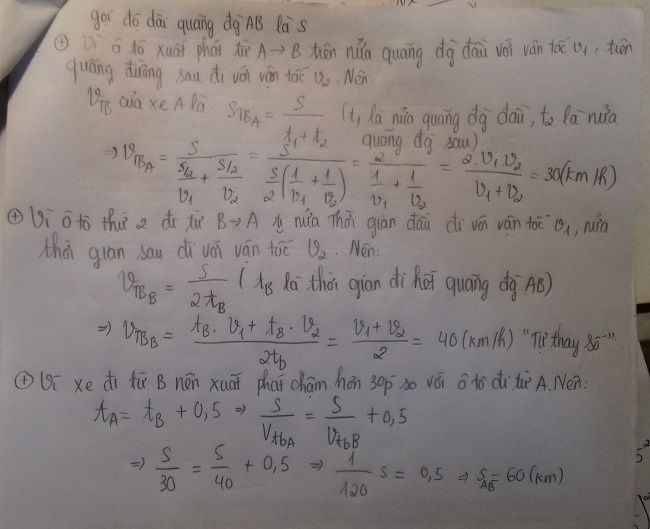
Cảm ơn nha