Cho tam giác ABC biết BAC = 60,AD là đường phân giác ( D thuộc BC) trên nửa mặt phẳng bờ BC chứa điểm A ve ACx=30 .Chứng minh AD song song với Cx
Nhớ vẽ thêm hình nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
IM
2 tháng 8 2016
Gọi Am là tia phân giác của góc A ; Cn là tia phân giác của góc C
Ta có
\(\widehat{BAC}=\widehat{ACx}\) (Cx//AB ; hai góc so le trong )
Mặt khác
\(\widehat{A1}=\frac{1}{1}\widehat{BAC}\)( Am là tia phân giác )
\(\widehat{C1}=\frac{1}{2}\widehat{ACx}\) ( Cn là tia phân giác )
\(\Rightarrow\widehat{A1}=\widehat{C1}\)
Mà \(\widehat{A1};\widehat{C1}\) so le trong
=> Am//Cn (đpcm)
KW
2 tháng 8 2016
bạn Silver bullet ơi , dòng thứ 4 từ câu mặt khác của bn ở dưới mk thay như vậy đc ko bn ?
A1=1.BAC(...)
C1=2.ACX(...)
NHƯ VẬY ĐC KO BN ?
6 tháng 1 2022
a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
Suy ra: BD=CD
b: Ta có: ΔABC cân tại A
mà AD là tia phân giác
nên AD là đường cao
11 tháng 11 2018
Bạn tự vẽ hình nhé
a) Xét \(\Delta ABD\)và\(\Delta ACD\)có:
AB = AC ( gt)
\(\widehat{BAD}=\widehat{CAD}\)(gt)
AD chung
\(\Rightarrow\)\(\Delta ABD=\Delta ACD\left(c.g.c\right)\)
CM
31 tháng 3 2018
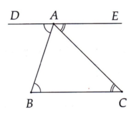
a) Có B A D ^ = A B C ^ ( giả thiết),
Mà hai góc ở vị trí so le trong nên AD // BC (theo tính chất hai đường thẳng song song).
b) Tương tự ý a), chứng minh được AE // BC
Theo tiên đề ơ-clit, hai đường thẳng AE và AD trùng nhau. Từ đó ba điểmD, A, E thẳng hàng.
CM
12 tháng 5 2017
a) Có B A D ^ = A B C ^ ( giả thiết),
Mà hai góc ở vị trí so le trong nên AD // BC (theo tính chất hai đường thẳng song song).
a) Tương tự ý a), chứng minh
b) được AE // BC
Theo tiên đề ơ-clit, hai đường thẳng AE và AD trùng nhau. Từ đó ba điểm D, A, E thẳng hàng
Lưu ý : nếu ai có cau trả lời hay nhất và hình đúng nhất thì mình cho
Có 2 cách vẽ tia Cx như 2 hình vẽ sau ban nhé: