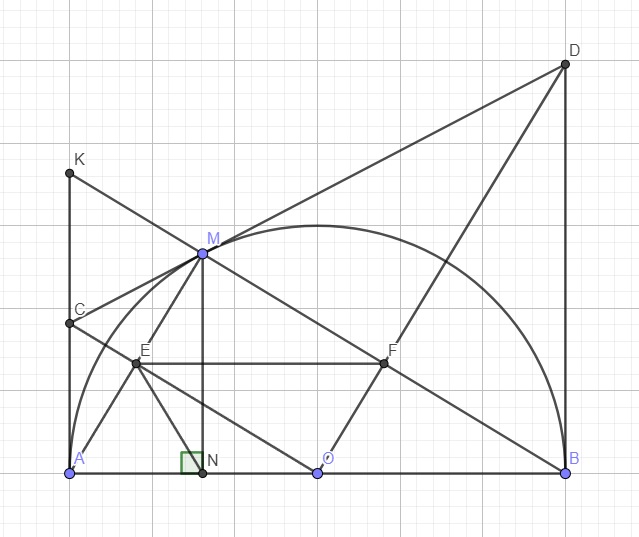
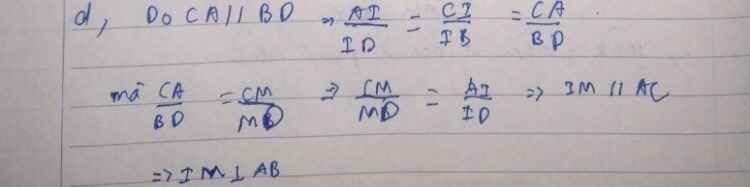Cho nửa đường tròn đường kính AB. Kẻ hai tia tiếp tuyến Ax và By với nửa đường tròn. C là
một điểm nằm trên nửa đường tròn. Tiếp tuyến với nửa đường tròn tại C cắt Ax, By tại M, N.
AN cắt BM tại I. Nối CI kéo dài cắt AB tại E. Chứng minh rằng:
1. MN = AM + BN
2. CI vuông góc với AB
3. I là trung điểm CE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 11 2022
Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
mà OM=OA
nên OC là đường trung trực của MA
=>OC vuông góc với MA tại I
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
mà OM=OB
nên OD là trung trực của BM
=>OD vuông góc với BM
Từ (1) và (2) suy ra góc COD=1/2*180=90 độ
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2023
C là giao điểm 2 tiếp tuyến tại A và M \(\Rightarrow OC\) là trung trực AM
\(\Rightarrow E\) là trung điểm AM
Tương tự ta có OD là trung trực BM \(\Rightarrow F\) là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác ABM
\(\Rightarrow EF||AB\Rightarrow ONEF\) là hình thang (1)
Lại có O là trung điểm AB \(\Rightarrow OF\) là đường trung bình tam giác ABM
\(\Rightarrow OF=\dfrac{1}{2}AM=AE\)
Mà \(OF||AE\) (cùng vuông góc BM)
\(\Rightarrow AEFO\) là hình bình hành \(\Rightarrow\widehat{OFE}=\widehat{OAE}\)
Mà \(EN=AE=\dfrac{1}{2}AM\Rightarrow\Delta AEN\) cân tại E \(\Rightarrow\widehat{OAE}=\widehat{ANE}\)
\(\widehat{ANE}+\widehat{ONE}=180^0\Rightarrow\widehat{OFE}+\widehat{ONE}=180^0\)
Lại có \(\widehat{ONE}+\widehat{NEF}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{OFE}=\widehat{NEF}\)
\(\Rightarrow ONEF\) là hình thang cân
4 tháng 10 2021
a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: CM+MD=CD
mà CM=CA
và DM=DB
nên CD=CA+DB
18 tháng 2 2022
a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: OC là tia phân giác của góc MOA(1)
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
DO đó; OD là tia phân giác của góc MOB(2)
Từ (1) và (2) suy ra \(\widehat{DOC}=\dfrac{1}{2}\left(\widehat{MOA}+\widehat{MOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
hay ΔODC vuông tại O
b: Xét ΔODC vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
21 tháng 11 2022
a: Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
mà OM=OA
nên OC là đường trung trực của MA
=>OC vuông góc với MA tại I
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
mà OM=OB
nên OD là trung trực của BM
=>OD vuông góc với BM
Từ (1) và (2) suy ra góc COD=1/2*180=90 độ
=>O nằm trên đường tròn đường kính CD
b: Xét tứ giác MIOK có
góc MIO=góc IOK=góc MKO=90 độ
nên MIOK là hình chữ nhật
=>MO=IK
c: Xét hình thang ABDC có
O,O' lần lượt là trung điểm của AB,CD
nên OO' là đường trung bình
=>OO''//AC
=>OO' vuông góc với AB
=>AB là tiếp tuyến của (O')