cho hai số dương a và thỏa mãn a*b=1. Tìm giá trị nhỏ nhất của biểu thức B=1/a + 1/b +2/a+b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


vì (a-1)2 ≥ 0 nên a2 +1 ≥ 2a ∀mọi x (1)
vì (b-1)2 ≥ 0 nên b2 +1 ≥ 2b ∀ mọi x (2)
từ 1 và 2 ⇒ a2+b2 ≥ 2a+2b
⇒ A≥ 2(a+b)=2
dấu''=' xảy ra khi a=b=1/2

Ta thấy \(ab\le\dfrac{a^2+b^2}{2}=1\) và \(a+b\le\sqrt{2\left(a^2+b^2\right)}=2\). Áp dụng BĐT B.C.S, ta được \(P=\dfrac{a^4}{ba^2+a^2}+\dfrac{b^4}{ab^2+b^2}\) \(\ge\dfrac{\left(a^2+b^2\right)^2}{ba^2+ab^2+a^2+b^2}=\dfrac{2^2}{ab\left(a+b\right)+2}\ge\dfrac{4}{1.2+2}=1\)
ĐTXR \(\Leftrightarrow a=b=1\)
Vậy GTNN của P là 1 khi \(a=b=1\)

Áp dụng bđt : 1/a + 1/b >= 4/a+b thì :
p = 1/a + 1/b >= 4/a+b >= 4/\(2\sqrt{2}\)= \(\sqrt{2}\)
Dấu "=" xảy ra <=> a=b=\(\sqrt{2}\)
Vậy ...............
Tk mk nha
Cho hai số a,b thỏa mãn a^2+b^2=1. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: A=a^6+b^6

\(A=a^6+b^6=\left(a^2\right)^3+\left(b^2\right)^3\)
\(=\left(a^2+b^2\right)\left(a^4+b^4-a^2b^2\right)\)
\(=1.\left[\left(a^4+b^4+2a^2b^2\right)-3a^2b^2\right]\)
\(=\left(a^2+b^2\right)^2-3a^2b^2\)
\(=1^2-3a^2b^2\)
\(\left(a-b\right)^2\ge0\Rightarrow a^2+b^2-2ab\ge0\Rightarrow\frac{a^2+b^2}{2}\ge ab\)
\(\Rightarrow ab\le1:2=0,5\Rightarrow3a^2b^2\le\frac{3}{4}\)
\(\Rightarrow A=1^2-3a^2b^2\ge1-\frac{3}{4}=\frac{1}{4}\)
\(\Rightarrow MinA=\frac{1}{4}\Leftrightarrow a=b=\frac{1}{2}\)
Vậy ...

Chọn B.
Ta có 6 ≤ log2(a + 1) + log2(b + 1) = log2[(a + 1)(b + 1) ]
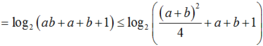
Suy ra: ![]() hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
Tương đương: (a + b) 2 + 4(a + b) - 252 ≥ 0
Suy ra: a + b ≥ 14
Áp dụng \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)và \(x+y\ge2.\sqrt{xy}\)( dấu ''='' xảy ra ở 2 bđt này khi x=y )
Ta có \(B=\frac{1}{a}+\frac{1}{b}+\frac{2}{a+b}\ge\frac{4}{a+b}+\frac{2}{a+b}=\frac{6}{a+b}\)
\(=\frac{6}{a+b}+\frac{3\left(a+b\right)}{2}-\frac{3.\left(a+b\right)}{2}\ge2\sqrt{\frac{6}{a+b}.\frac{3\left(a+b\right)}{2}}-\frac{3.2.\sqrt{ab}}{2}\)
\(=2\sqrt{9}-3.\sqrt{ab}=6-3=3\)
Dấu ''='' xảy ra khi \(\hept{\begin{cases}\frac{6}{a+b}=\frac{3.\left(a+b\right)}{2}\\a=b\\a.b=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{6}{2a}=\frac{3.2a}{2}\\a=b\\a.b=1\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}12a^2=12\\a=b\\a.b=1\end{cases}}\)\(\Leftrightarrow a=b=1\)