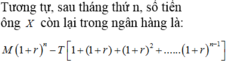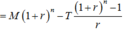1 học sinh muốn có 5 triệu để đi mua điện thoại nhưng ko đủ tiền . Bạn ấy quyết định gửi ngân hàng với lãi xuất 0.6%/tháng . tháng đầu tiên gửi 100 nghìn , kể từ tháng thứ 2 trở đi chỉ gửi 20 nghìn . Hỏi sau bao nhiêu tháng thì đủ số tiền trên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 10 2023
Gọi số tiền bạn Niên phải gửi là x(đồng)(ĐK: x>0)
Tháng thứ nhất bạn Niên nhận được là \(x\cdot\left(1+0.27\%\right)\left(đồng\right)\)
Số tiền nhận được sau 2 tháng là:
\(\left[x\left(1+0.27\%\right)+x\right]\cdot\left(1+0.27\%\right)\)
\(=x\cdot\left(1+0.27\%\right)^2+x\cdot\left(1+0.27\%\right)\)
Theo đề, ta có:
\(x\cdot\left(1+0.27\%\right)^{12}+x\cdot\left(1+0.27\%\right)^{11}+...+x\cdot\left(1+0.27\%\right)=20000000\)
=>\(x\cdot\left(1+0.27\%\right)\cdot\left[\left(1+0.27\%\right)^{11}+\left(1+0.27\%\right)^{10}+...+1\right]=20000000\)
=>\(x\cdot\left(1+0.27\%\right)\cdot\dfrac{1-\left(1+0.27\%\right)^{11}}{1-\left(1+0.27\%\right)}=20000000\)
=>\(x\simeq1788939\)(đồng)
31 tháng 12 2023
-Gọi số tiền sinh viên A có được sau n tháng là \(u_n\) (đồng) (\(u_n>0;n\in N\cdot\)).
-Theo đề bài, ta có: \(\left\{{}\begin{matrix}u_1=2.10^6\left(đồng\right)\\u_{n+1}=\left(100\%+0,6\%\right)u_n+10^5=1,006u_n+10^5\left(1\right)\end{matrix}\right.\)
(NHÁP:
-Ta sẽ tạo ra dãy cấp số nhân có liên hệ với (1). Để làm vậy, trước tiên đặt \(v_n=u_n-a\Rightarrow u_n=v_n+a\) (a là hằng số).
Khi đó \(v_{n+1}+a=1,006\left(v_n+a\right)+10^5\)
\(\Rightarrow v_{n+1}=1,006v_n+\left(1,006a-a+10^5\right)\)
Để tạo thành cấp số nhân, \(1,006a-a+10^5=0\), giải ra ta được: \(a=\dfrac{-5.10^7}{3}\))
*Đặt \(v_n=u_n+\dfrac{5.10^7}{3}\Rightarrow u_n=v_n-\dfrac{5.10^7}{3}\). Thế vào (1) ta được:
\(v_{n+1}=1,006v_n\) => \(\left(v_n\right)\) là cấp số nhân với \(q=1,006\)
Ta lại có: \(v_1=u_1+\dfrac{5.10^7}{3}=2.10^6+\dfrac{5.10^7}{3}\)
\(\Rightarrow v_n=\left(2.10^6+\dfrac{5.10^7}{3}\right).1,006^{n-1}\)
\(\Rightarrow u_n=\left(2.10^6+\dfrac{5.10^7}{3}\right).1,006^{n-1}-\dfrac{5.10^7}{3}\)
Vậy sau 12 tháng sinh viên A có:
\(u_{12}=\left(2.10^6+\dfrac{5.10^7}{3}\right).1,006^{11}-\dfrac{5.10^7}{3}=3.269.633,331\left(đồng\right)\)
CM
30 tháng 3 2018
Chọn B.
Khi anh T gửi ngân hàng A:
*Trong 12 tháng đầu tiên số tiền anh T có là
T12 = a(1 + r)n = 180.(1 + 0,012) 12 = 207,7 triệu đồng
*Trong 6 tháng còn lại số tiền anh T có cả gốc lẫn lãi là
TA = 207,7( 1 + 0,01) 6 = 220,5 triệu đồng
Khi anh T gửi ngân hàng B:
*Cuối tháng thứ 18, anh T có số tiền cả gốc lẫn lãi là
*Với m = 0,8%; n = 18; a = 10 triệu đồng.
Suy ra 
triệu đồng
Do đó TA - TB = 26,2 triệu đồng.