Từ một số tự nhiên n có 3 chữ số cho trước , ta sẽ được số nào nếu: viết thêm vào số 0 vào tận cùng bên phải số đó và số một cũng vậy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta sẽ được một số gấp 10 lần số n
b) Ta sẽ được một số lớn hơn số n 1000 đơn vị

a) Nếu viết thêm chữ số 0 vào sau ( tận cùng bên phải ) số đó thì ta được số mới gấp 10 lần số đã cho
b) Nếu viết thêm chữ số 1 vào trước ( tận cùng bên trái ) số đó thì ta được số mới gấp 11 lần số đã cho

thì số đó sẽ gấp lên 10 lần
VD: 1 thêm số 0 là 10
10 gấp 1 10 lần

gọi số ban đầu là x, chữ số thêm vào là y
khi đó ta có số mới có giá trị là \(10\times x+y\)
ta có :\(10\times x+y-x=11139\)
hay \(9\times x+y=11139\text{ hay }9x=11139-y\)
nên \(11139-y\text{ chia hết cho 9}\) mà y là chữ số nên \(0\le y\le9\)
\(\Rightarrow y=6\Rightarrow x=1237\)
vậy số đã cho là 1237 và số thêm vào là 6

Khi viết thêm số 0 vào tận cùng bên phải ta sẽ được số mới gấp 10 lần số cần tìm.
Cho số cần tìm là 1 phần thì số mới là 10 phần. Hiệu số phần bằng nhau là:
10 - 1 = 9 (phần)
Số cần tìm là:
2574 : 9 = 286
Đáp số: 286.

Gọi số đó là x
Ta có: \(\overline{x0}-x=1125\)
\(10x-x=1125\)
\(9x=1125\)
\(=>x=125\)
=> sô cần tìm là 125
Khi viết thêm chữ số \(0\) vào tận cùng bên phải của một số thu được số mới gấp \(10\) lần số ban đầu.
Nếu số cần tìm là \(1\) phần thì số mới là \(10\) phần.
Hiệu số phần bằng nhau là:
\(10-1=9\) (phần)
Số cần tìm là:
\(1125\div9\times1=125\)

Viết chữ số 0 vào tận cùng bên phải của một số thì số đó gấp lên 10 lần
Số phải tìm là:
4212 : (10 - 1) = 468
Đáp số: 468
Gọi số cần tìm là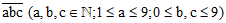
Khi viết thêm chữ số 0 vào bên phải số đó ta được số: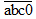
Ta có: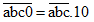
Vậy nếu viết thêm chữ số 0 vào sau (tận cùng bên phải) số đó ta được số mới gấp 10 lần số đã cho.
Còn số 1 nữa