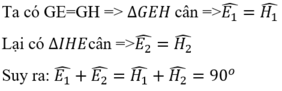Giúp mình bài này với ạ
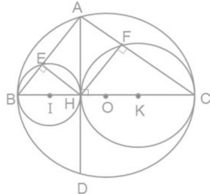
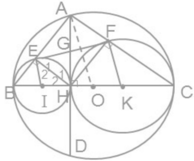
Cho đường tròn tâm (O) đường kính BC,dây AD vuông góc với BC tại H. Gọi E,F theo thứ tự là chân đường vuông góc kẻ từ H đến AB,AC.Gọi (I) (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE,HCF.
a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).
b) tứ giác AEHF là hình gì? vì sao?
c) chứng minh đẳng thức AE.AB=AF.AC
d) chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K)
e) xác định vị trí của điểm H để EF có độ dài lớn nhất.
Giúp mình giải câu d) và e) với, mình cảm ơn