Tìm GTNN của A = 4x4 + 4x2 - 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


C3 : Ta có ; \(B=\sqrt{x-4}+\sqrt{y-3}\) . Nhận xét : \(B\ge0\)
- Áp dụng bất đẳng thức Bunhiacopxki : \(B^2=\left(1.\sqrt{x-4}+1.\sqrt{y-3}\right)^2\le\left(1^2+1^2\right)\left(x-4+y-3\right)\)
\(\Rightarrow B^2\le16\Rightarrow B\le4\). Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x\ge4,y\ge3\\\sqrt{x-4}=\sqrt{y-3}\\x+y=15\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=8\\y=7\end{cases}}\)
Vậy B đạt giá trị lớn nhất bằng 4 tại (x;y) = (8;7)
Tìm GTNN và mấy bài tới để từ từ mình làm cho nhé , tại mạng đang chậm...
C4 : Bạn cần thêm điều kiện x là số dương nhé : )
Ta có ; \(A=\frac{2x^2-6x+5}{2x}=x+\frac{5}{2x}-3\). Áp dụng bất đẳng thức Cauchy :
\(x+\frac{5}{2x}\ge2\sqrt{x.\frac{5}{2x}}=\sqrt{10}\). Dấu "=" xảy ra \(\Leftrightarrow x=\frac{5}{2x}\Leftrightarrow\sqrt{\frac{5}{2}}\)
Vậy Min A = \(\sqrt{10}-3\Leftrightarrow x=\sqrt{\frac{5}{2}}\)
C5 : Bạn cần thêm điều kiện a,b là hằng số nhé :)
\(P=\frac{\left(x+a\right)\left(x+b\right)}{x}=\frac{x^2+ax+bx+ab}{x}=x+\frac{ab}{x}+a+b\)
Áp dụng bất đẳng thức Cauchy : \(x+\frac{ab}{x}\ge2\sqrt{x.\frac{ab}{x}}=2\sqrt{ab}\Rightarrow P\ge a+2\sqrt{ab}+b=\left(\sqrt{a}+\sqrt{b}\right)^2\)
Dấu "=" xảy ra khi và chỉ khi \(x^2=ab\Leftrightarrow x=ab\) (vì a,b,x > 0)
Vậy .......

\(A=\left(x-4\right)\left(x+3\right)\)
\(=x^2-x-12\)
\(=x^2-x+\dfrac{1}{4}-\dfrac{49}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2-\dfrac{49}{4}\ge-\dfrac{49}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)

\(C=4x^2+y^2-4x+8y+12\)
\(C=4x^2-4x+1+y^2+8y+16-5\)
\(C=\left(4x^2-4x+1\right)+\left(y^2+8y+16\right)-5\)
\(C=\left(2x-1\right)^2+\left(y+4\right)^2-5\)
Mà: \(\left\{{}\begin{matrix}\left(2x-1\right)^2\ge0\forall x\\\left(y+4\right)^2\ge0\forall x\end{matrix}\right.\)
Nên: \(C=\left(2x-1\right)^2+\left(y+4\right)^2-5\ge-5\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}2x-1=0\\y+4=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-4\end{matrix}\right.\)
Vậy: \(C_{min}=-5\) khi \(\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-4\end{matrix}\right.\)

a) Vì \(\left(2x+\frac{1}{4}\right)^4\ge0\forall x\)
\(\Rightarrow A\ge1\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow2x+\frac{1}{4}=0\Leftrightarrow x=\frac{-1}{8}\)
b) \(B=-\left(\frac{4}{9}x-\frac{2}{15}\right)^6+3\)
\(B=3-\left(\frac{4}{9}x-\frac{2}{15}\right)^6\)
Vì \(\left(\frac{4}{9}x-\frac{2}{15}\right)^6\ge0\forall x\)
\(\Rightarrow B\le3\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow\frac{4}{9}x-\frac{2}{15}=0\Leftrightarrow x=\frac{3}{10}\)
với mọi x thì (2x+1/4)4>=0 (lớn hơn hoặc bằng )
A=(2x+1/4)4-1>=-1
để A đạt GTNN thì (2x+1/4)4=0
2x+1/4=0 =>x=-1/8


Chọn đáp án B
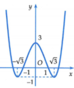
Ta có
![]()
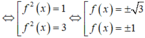
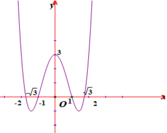
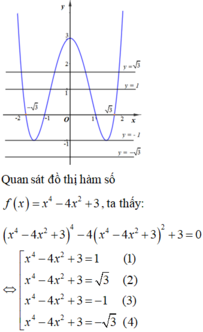
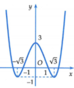
Quan sát đồ thị của hàm số y = f(x) ta thấy:
Phương trình f x = - 3 không có nghiệm; phương trình f x = - 1 có 2 nghiệm;
phương trình f x = 1 có 4 nghiệm; phương trình f x = 3 có 4 nghiệm.
Vậy phương trình x 4 - 4 x 2 + 3 2 - 4 x 4 - 4 x 2 + 3 2 + 3 = 0 có 10 nghiệm.

d. A(x) = M(x) + 2N(x)
= 10x3 + 5x2 - 4x - 1 + 2(x2 - 9)
= 10x3 + 7x2 - 4x - 19 (0.5 điểm)
Thay x = 1 vào biểu thức ta có: A(1) = -6 (0.5 điểm)


\(A=4x^4+4x^2-3\)
\(A=\left[\left(2x^2\right)^2+2.2x^2.1+1^2\right]-4\)
\(A=\left(2x+1\right)^2-4\)
Ta có: \(\left(2x+1\right)^2\ge0\forall x\)
\(\Rightarrow\left(2x+1\right)^2-4\ge-4\forall x\)
\(A=-4\Leftrightarrow\left(2x+1\right)^2=0\Leftrightarrow x=-\frac{1}{2}\)
Vậy \(A_{min}=-4\Leftrightarrow x=-\frac{1}{2}\)