Giúp mình bài này với, mình đang gấp lắm lắm Cho hàm số y=(1-m).x m 3 (1) A. Tìm m để hàm số (1) là hàm số bậc nhất. B. Tìm m để hàm số (1) là hàm số nghịch biến. C. Tìm m biết rằng đồ thị hàm số (1)...

BÀI 1 : cho hàm số bậc nhất y=mx+1 với m là tham số . tìm m để đồ thị hàm số đi qua điểm A(1;4). với giá trị m vừa tìm được ,hàm số đồng biến hay nghịch biến

#Toán lớp 9

3

NL

Nguyễn Lê Phước Thịnh

11 tháng 9 2021

Thay x=1 và y=4 vào (d), ta được:

m+1=4

hay m=3

Vậy: Hàm số đồng biến trên R

Đúng(1)

NV

Nguyễn Việt Lâm

Giáo viên

11 tháng 9 2021

Do đồ thị hàm số qua A, thay tọa độ A vào phương trình ta được:

\(4=m.1+1\Rightarrow m=3\)

\(\Rightarrow y=3x+1\)

Do \(a=3>0\Rightarrow\) hàm số đồng biến

Đúng(1)

TP

Thang phan huu

5 tháng 8 2023

Cho hàm số y=(3-m) x +2 a, Tìm M để hàm số đã cho là hàn số bậc nhất b, Tìm m để hàm số đã cho có nghịch biến c, Tìm m để giá trị hàm số đã cho đi qua điểm Ac( 2,3) d, Tìm m để đồ thị hàm số đã cho đi qua điểm B(-1;-5)

#Toán lớp 9

1

KV

Kiều Vũ Linh

5 tháng 8 2023

a) Để hàm số là hàm bậc nhất thì 3 - m 0

m 3

b) Để hàm số là nghịch biến thì 3 - m < 0

m > 3

c) Thay tọa độ điểm A(2; -3) vào hàm số, ta được:

(3 - m).2 + 2 = -3

6 - 2m + 2 = -3

8 - 2m = -3

2m = 11

m = 11/2 (nhận)

Vậy m = 11/2 thì đồ thị hàm số đi qua A(2; -3)

(Sửa theo yêu cầu rồi nhé em!)

d) Thay tọa độ B(-1; -5) vào hàm số, ta được:

(2 - m).(-1) + 2 = -5

-2 + m + 2 = -5

m = -5 (nhận)

Vậy m = -5 thì đồ thị hàm số đi qua B(-1; -5)

Đúng(1)

TP

Thang phan huu

5 tháng 8 2023

Chị ơi câu c điểm A( 2; -3) chị ạ

Đúng(0)

TM

Trần Mun

25 tháng 12 2023

Bài 4: Cho hàm số y = (1 - m)x + m - 2a) Tìm điều kiện để hàm số trên là hàm số bậc nhấtb) Tìm m để hàm số nghịch biếnc) Tìm m để đồ thị hàm số song song với đường thẳng y = 2x - 3d) Tìm m để đồ thị hàm số cắt đường thẳng y = -x + 1e) Tìm m để đồ thị hàm số đi qua điểm A(2;1)g) Tìm m để đồ thị hàm số tạo với trục Ox một góc nhọn, một góc tùh) Tìm m để đồ thị hàm số cắt trục tung tại...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

25 tháng 12 2023

a: Để hàm số y=(1-m)x+m-2 là hàm số bậc nhất thì \(1-m\ne0\)

=>\(m\ne1\)

c: Để đồ thị hàm số y=(1-m)x+m-2 song song với đường thẳng y=2x-3 thì

\(\left\{{}\begin{matrix}1-m=2\\m-2\ne-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m=-1\\m\ne-1\end{matrix}\right.\)

=>\(m\in\varnothing\)

d: Để đồ thị hàm số y=(1-m)x+m-2 cắt đường thẳng y=-x+1 thì \(1-m\ne-1\)

=>\(m\ne2\)

e: Thay x=2 và y=1 vào y=(1-m)x+m-2, ta được:

2(1-m)+m-2=1

=>2-2m+m-2=1

=>-m=1

=>m=-1

g: Để đồ thị hàm số y=(1-m)x+m-2 tạo với trục Ox một góc nhọn thì 1-m>0

=>m<1

Để đồ thị hàm số y=(1-m)x+m-2 tạo với trục Oy một góc tù thì 1-m<0

=>m>1

h: Thay x=0 và y=3 vào y=(1-m)x+m-2, ta được:

0(1-m)+m-2=3

=>m-2=3

=>m=5

f: Thay x=-2 và y=0 vào y=(1-m)x+m-2, ta được:

-2(1-m)+m-2=0

=>-2+2m+m-2=0

=>3m-4=0

=>3m=4

=>\(m=\dfrac{4}{3}\)

Đúng(0)

TM

Trần Mun

24 tháng 12 2023

Bài 4: Cho hàm số y = (1 - m)x + m - 2a) Tìm điều kiện để hàm số trên là hàm số bậc nhấtb) Tìm m để hàm số nghịch biếnc) Tìm m để đồ thị hàm số song song với đường thẳng y = 2x - 3d) Tìm m để đồ thị hàm số cắt đường thẳng y = -x + 1e) Tìm m để đồ thị hàm số đi qua điểm A(2;1)g) Tìm m để đồ thị hàm số tạo với trục Ox một góc nhọn, một góc tùh) Tìm m để đồ thị hàm số cắt trục tung tại...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

25 tháng 12 2023

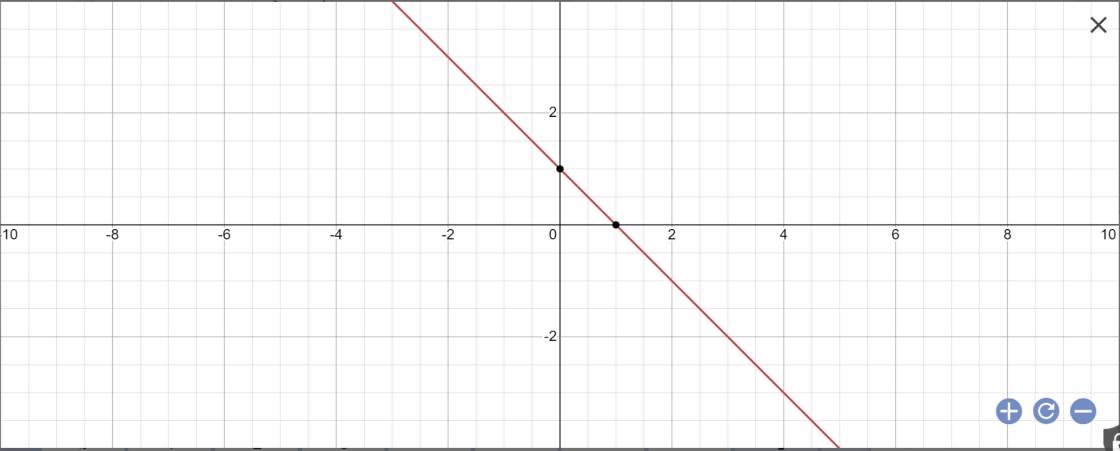
loading...

b: Để hàm số y=(1-m)x+m-2 nghịch biến trên R thì 1-m<0

=>m>1

Đúng(0)

DT

Dương Thị Như Ý

26 tháng 9 2023

# Bài 24. Cho hai đường thẳng (D): y = (m − 2)x + 1& (D0 ) : y = m2 x − 2x + m. 1) Tìm m để (D) là hàm số bậc nhất? Hàm số đồng biến? Hàm số nghịch biến? 2) Tìm m biết (D) // (D’). 3) Với m tìm được ở câu 2 hãy a) Vẽ đồ thị (D); b) Tính góc tạo bởi đường thẳng (D) và trục Ox; c) Tính chu vi và diện tích tam giác được tạo bởi đường thẳng (D), Ox, Oy; d) Tính khoảng cách từ gốc tọa độ O đến đường thẳng...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

17 tháng 11 2023

1: (D): y=(m-2)x+1

(D'): \(y=m^2x-2x+m=x\left(m^2-2\right)+m\)

Để (D) là hàm số bậc nhất thì m-2<>0

=>m<>2

Để (D): y=(m-2)x+1 đồng biến trên R thì m-2>0

=>m>2

Để (D): y=(m-2)x+1 nghịch biến trên R thì m-2<0

=>m<2

2: Để (D)//(D') thì \(\left\{{}\begin{matrix}m^2-2=m-2\\m< >1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m^2-m=0\\m< >1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\m< >1\end{matrix}\right.\)

=>m=0

3:

a: Khi m=0 thì (D): y=(0-2)x+1=-x+1

loading...

b: Gọi \(\alpha\) là góc tạo bởi (D) với trục Ox

Ta có: a=-1

nên \(tan\left(180^0-\alpha\right)=-1\)

=>\(180-\alpha=135^0\)

=>\(\alpha=45^0\)

4:

Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}2x-8=-x+1\\y=2x-8\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x=9\\y=2x-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\cdot3-8=-2\end{matrix}\right.\)

Thay x=3 và y=-2 vào (D), ta được:

\(3\left(m-2\right)+1=-2\)

=>3(m-2)=-3

=>m-2=-1

=>m=1

5: Để (D) cắt (D') tại một điểm trên trục hoành thì

\(\left\{{}\begin{matrix}m-2< >m^2-2\\-\dfrac{1}{m-2}=\dfrac{-m}{m^2-2}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m^2-m\ne0\\\dfrac{1}{m-2}=\dfrac{m}{m^2-2}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m\left(m-1\right)\ne0\\m^2-2=m^2-2m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\notin\left\{0;1\right\}\\-2m=-2\end{matrix}\right.\)

=>\(m\in\varnothing\)

6: (D): y=(m-2)x+1

=>y=mx-2x+1

Điểm mà (D) luôn đi qua có tọa độ là:

\(\left\{{}\begin{matrix}x=0\\y=-2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0+1=1\end{matrix}\right.\)

Đúng(0)

NL

NGUYỄN LINH NY

18 tháng 7 2018 - olm

Cho hàm số: y=(2m - 1)x

a) Xác định m để đồ thị hàm số đi qua điểm A(1;-2)

b) Vẽ đồ thị hàm số ứng với m vừa tìm được

Giúp mình với mình cần gấp lắm... mai là mình phải nộp bài rồi

#Toán lớp 7

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP