cho tam giác ABC có A=60° Vẽ tia phân giác của góc A cắt BC tại D Từ B vẽ đường thẳng xy song song với AD tính số đo góc ABx và ABy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
4 tháng 12 2023
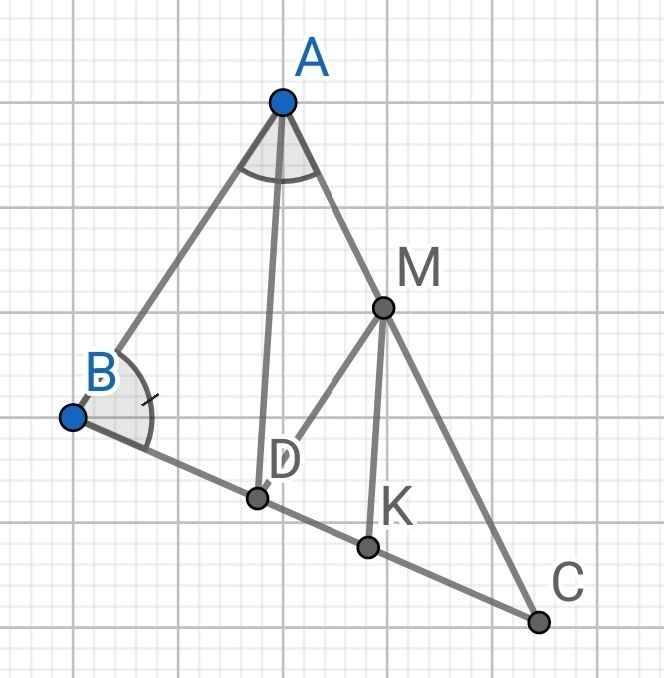
Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠DAM = 60⁰ : 2 = 30⁰
Do DM // AB (gt)
⇒ ∠ADM = ∠BAD = 30⁰ (so le trong)
Do DM // AB (gt)
⇒ ∠MDK = ∠B = 80⁰ (đồng vị)
⇒ ∠ADK = ∠ADM + ∠MDK
= 30⁰ + 80⁰
= 110⁰
21 tháng 8 2023
góc C=180 độ-góc A-góc B
=180-60-80=40 độ
MD//AB
=>góc ADM=góc BAD=60/2=30 độ
DM//AB
=>góc DMC=góc BAC=60 độ
30 tháng 9 2015
a) Vì AB// MD suy ra BAD= MDA (so le) ; AD// MK suy ra ADM= KDM (so le)
nên BAD= ADM= DMK
b) Vì BAD= DMK (câu a) mà BAD= KMC (đồng vị vì AD// MC)
nên DMK= CMK suy ra MK là phân giác DMC
tích đúng cho mình nhé
4 tháng 8 2019
a) Vì AD là phân giác BAC
=> BAD = CAD = \(\frac{60°}{2}\)= 30°
Vì AB//DM
=> BAD = ADM = 30° ( so le trong)
Vì AD//MK
=> ADM = DMK = 30° ( so le trong)
b) Mà AD//MK
=> DAC = KMC = 30° ( đồng vị)
=> DMK = KMC = 30°
Hay MK là phân giác DMC
10 tháng 9 2021
\(a,\widehat{A}+\widehat{B}+\widehat{C}=180\\ \Rightarrow180-3\widehat{C}+\widehat{C}+70=180\\ \Rightarrow-2\widehat{C}=-70\\ \Rightarrow\widehat{C}=35\\ \Rightarrow\widehat{A}=180-35=145\)
Lời giải:
Vì $\widehat{BAC}=60^0$ và $AD$ là tia phân giác $\widehat{A}$ nên $\widehat{BAD}=\frac{1}{2}\widehat{BAC}=30^0$
Theo hình vẽ $Bx\parallel AD$ nên $\widehat{ABx}=\widehat{BAD}=30^0$ (hai góc so le trong)
$\widehat{ABy}=180^0-\widehat{ABx}=180^0-30^0=150^0$
Hình vẽ: