cho hình vuông ABCD , M là trung điểm AB, N là trung điểm BC , AN cắt CM tại O . Tính tỉ số S(aocd)/S(abcd)
Ai giải giúp mik với mik tích cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác L BCM = tam giác L CDN (2 cạnh góc L = nhau)
=> CDN^ = BCM^
lại có:
BMC^ = DCI^ (so le trong)
=> CID^ =CBM^ = 1v (xét 2 tam giác CDI và CBM)
gọi P là trung điểm của CD và Q là giao điểm của AP và DN
ta có tứ giác AMCP là hình bình hành vì có AM//=CP
=> AP // CM
=> AP L DN
xét tam giác DCI có P là trung điểm của CD và PQ // CI nên Q là trung điểm của DI
vậy AQ là đường cao vùa là trung tuyến của tam giác ADI => tam giác ADI cân tại A => AD=AI
~~~~~~~~~~~~~~~~~~~~ ai đi qua nhớ để lại ~~~~~~~~~~~~~~~~~~
Kéo dài BO cắt AC tại H.Nhận thấy O là trọng tâm tam giác ABC>>>BO=2/3BH.Mà BH dễ tính do tam giác ABC vuông cân.
>>>Tính được BO(nhớ k nha)

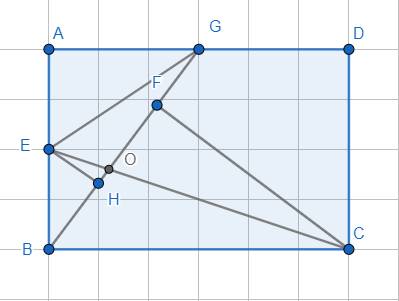
Kẻ \(EH\perp BG\), \(CF\perp BG\)
Ta có: \(S_{ABD}=S_{GBC}=\dfrac{1}{2}.AB.AD=\dfrac{1}{2}.S_{ABCD}\)
\(S_{BAG}=\dfrac{1}{2}.AB.AG=\dfrac{1}{2}.AB.\dfrac{1}{2}AD=\dfrac{1}{4}.AB.AD=\dfrac{1}{2}S_{ABD}\)
\(S_{GEB}=\dfrac{1}{2}.AG.EB=\dfrac{1}{2}.AG.\dfrac{1}{2}.AB=\dfrac{1}{4}.AG.AB=\dfrac{1}{2}S_{ABG}\)
\(\Rightarrow S_{GEB}=\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}S_{ABCD}=\dfrac{1}{8}S_{ABCD}=\dfrac{1}{4}S_{GBC}\)
\(\Leftrightarrow\dfrac{1}{2}.EH.BG=\dfrac{1}{4}.\dfrac{1}{2}CF.BG\)
\(\Leftrightarrow EH=\dfrac{1}{4}CF\)
Lại có: \(S_{OBE}=\dfrac{1}{2}OB.EH=\dfrac{1}{2}OB.\dfrac{1}{4}CF=\dfrac{1}{4}S_{OBC}\)
Ta có: \(S_{CBE}=S_{OBE}+S_{OBC}=S_{OBE}+4S_{OBE}=5S_{OBE}\)
\(S_{CBE}=5.10=50\left(cm^2\right)\)
Mà \(S_{CBE}=\dfrac{1}{2}S_{CBA}=\dfrac{1}{4}S_{ABCD}\Rightarrow S_{ABCD}=200\left(cm^2\right)\)