Một người đi xe đạp từ A đến B với vân tốc v = 12km/h . Nếu người đó tăng tốc lên 3km/h thì đến nơi sớm hơn 1h
a, Tìm quãng đường và thời gian dự định đi từ A đến B
b, Ban đầu người đó đi với vận tốc v1 = 12km/h được một quãng đường S1 thì dừng lại nghỉ mất 15 phút . Do đó trong quãng đường còn lại người ấy đi với vận tốc 15km/h thì đến nơi vẫn sớm hơn dự định 30 phút . Tìm...
Đọc tiếp
Một người đi xe đạp từ A đến B với vân tốc v = 12km/h . Nếu người đó tăng tốc lên 3km/h thì đến nơi sớm hơn 1h
a, Tìm quãng đường và thời gian dự định đi từ A đến B
b, Ban đầu người đó đi với vận tốc v1 = 12km/h được một quãng đường S1 thì dừng lại nghỉ mất 15 phút . Do đó trong quãng đường còn lại người ấy đi với vận tốc 15km/h thì đến nơi vẫn sớm hơn dự định 30 phút . Tìm quãng đường S1
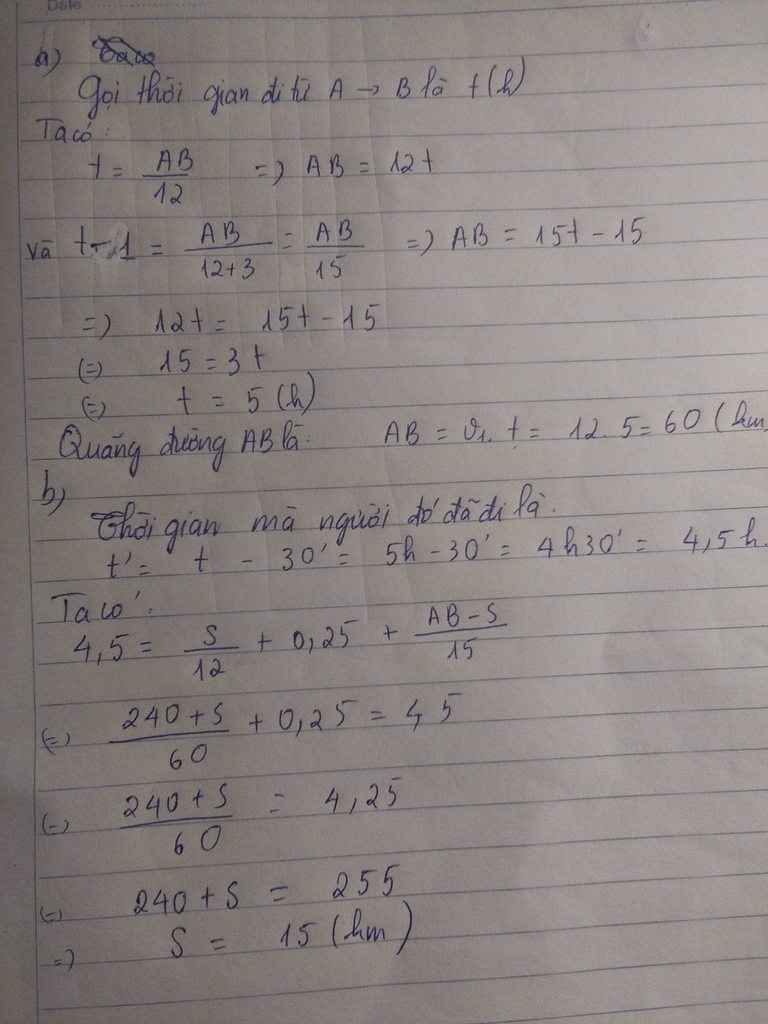
a) Thời gian dự đinh là \(t1=\dfrac{S}{12}h\)
Thời gian thực tế là \(t2=\dfrac{S}{15}h\)
Ta có \(\dfrac{S}{12}-\dfrac{S}{15}=1=>S=60km\)=>Thay vào tính t1=\(\dfrac{60}{12}=5h\)
b) Thời gian người đó đi là
\(t=\dfrac{S1}{12}+\dfrac{S-S1}{15}+\dfrac{15}{60}\)
Mặt khác ta có \(t1-t=\dfrac{30}{60}=>5-\dfrac{S1}{12}-\dfrac{60-S1}{15}-\dfrac{1}{4}=\dfrac{1}{2}=>S1=15km\)
Vậy..........
Vận tốc thực tế của người đó là :
\(v_{tt}=12+3=15\left(km/h\right)\)
Ta có bảng sau :
=> Phương trình : \(\dfrac{x}{12}-\dfrac{x}{15}=1\)
Gọi quãng đường AB là x(km). Đk : x >0
Thời gian dự kiến là :
\(t_{dk}=\dfrac{s}{v_{dk}}=\dfrac{x}{12}\left(h\right)\)
Thời gian thực tế mà người đó đi là :
\(t_{tt}=\dfrac{s}{v_{tt}}=\dfrac{x}{15}\left(h\right)\)
Vì nếu người đó tăng tốc lên 3km/h thì đến sớm hơn 1h nên ta có phương trình :
\(\dfrac{x}{12}-\dfrac{x}{15}=1\)
\(\Leftrightarrow\dfrac{15x}{180}-\dfrac{12x}{180}=\dfrac{180}{180}\)
\(\Rightarrow x=\dfrac{180}{15-12}=\dfrac{180}{3}=60\left(km\right)\)
Vậy quãng đường AB dài 60km, thời gian dự định đi từ A đến B là : \(t_{dk}=\dfrac{x}{12}=\dfrac{60}{12}=5\left(h\right)\)