Câu 5: Từ một điểm O trên nóc một bức tường có chiều cao h=5,00m, một quan sát viên nhìn thấy ảnh P’ của vật nhỏ P cách mặt đất một khoảng H (H>h) do anh sáng phản xạ trên một vũng nước nhỏ S nằm trên mặt đất nằm ngang cách chân tường một khoảng d= 5,00m. Để đo chiều cao H, quan sát viên đã đặt một gương phẳng G tại O sao cho mặt phản xạ hướng lên trên rồi xoay gương nay tới vị trí hợp với phương nằm ngang một góc α = 15,0֯thì thấy ảnh P’’ của P qua G ( do ánh sáng từ P rọi tới gương G và phản xạ trực tiếp trên G) nằm trên đường thẳng P’O. Sau đó quan sát viên lật mặt phản xạ của G hướng xuống rồi xoay nó tới vị trí hợp với phương nằm ngang một góc α’≠ α thì thấy ảnh P’’’ của P qua G ở vị trí này lại nằm trên đường thẳng P’O.
1. Tính chiều cao H.
2. Tìm α’.
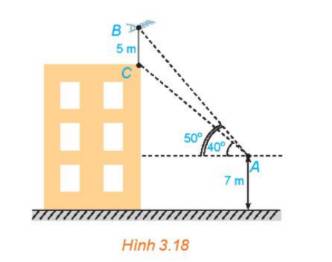
 CBA đồng dạng với
CBA đồng dạng với  =
= 

 =
= 
 CH =
CH =  = 4m
= 4m