(𝑥 − 3048): 145 = 236
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)<
b)>
c)<
Tìm x
a)X x 6 =3048:2
X =3048:2:6
X =254
B)56 :X =1326-1318
56 :X =8
X =56:8
X =7

* 123+123 -456
=246 - 456
= - 210
*145 - 236 + 125
= - 91 + 125
=34

b: Ta có: \(B=x^2\left(11x-2\right)+x^2\left(x-1\right)-3x\left(4x^2-x-2\right)\)
\(=11x^3-2x^2+x^3-x^2-12x^3+3x^2+6x\)
\(=6x\)

a: \(x\in\left\{25;30;35\right\}\)
b: \(x\in\left\{24;32;40;48;56;64\right\}\)
c: \(x\in\left\{3;4;6\right\}\)

1) Rút gọn biểu thức M: M = (2√x)/(√x - 3) - (x + 9√x)/(x - 9) = (2√x(x - 9) - (x + 9√x)(√x - 3))/(√x - 3)(x - 9) = (2x√x - 18√x - x√x + 9x + 9x - 27√x - 9√x + 27 )/(√x - 3)(x - 9) = (2x√x - 36√x + 27x)/(√x - 3)(x - 9) = (x(2√x - 36) + 27x) /(√x - 3)(x - 9) = (x(2√x - 36 + 27))/(√x - 3)(x - 9) = (x(2√x - 9))/( √x - 3)(x - 9) Do đó biểu thức M Rút gọn là: M = (x(2√x - 9))/(√x - 3)(x - 9) 2) Tìm các giá trị của x ă mãn M/N.(căn x + 3) = 3x - 5: Ta có phương trình: M/N.(căn x + 3) = 3x - 5 Đặt căn x + 3 = t, t >= 0, ta có x = t^2 - 3 Thay x = t^2 - 3 vào biểu thức M/N, ta có: M/N = [(t^2 - 3)(2√(t^2 - 3) - 9)]/[(t^2 - 3 + 5)t] = [(2(t^2 - 3) √(t^2 - 3) - 9(t^2 - 3))]/(t^3 + 2t - 3t - 6) = [2(t^2 - 3)√(t^2 - 3) - 9(t^2 - 3)]/(t(t - 1)(t + 2)) Đặt u = t^2 - 3, ta có: M/N = [2u√u - 9u]/((u + 3)(u + 2)) = [u(2√u - 9)]/((u + 3)(u + 2)) Đặt v = √u, ta có: M/N = [(v^ 2 + 3)(2v - 9)]/[((v^2 + 3)^2 - 3)(v^2 + 2)] = [(2v^3 - 18v + 6v - 54)]/[ ( (v^4 + 6v^2 + 9) - 3)(v^2 + 2)] = (2v^3 - 12v - 54)/(v^4 + 6v^2 + 6v^2 - 9v^2 + 18) = (2v^3 - 12v - 54)/(v^4 + 12v^2 + 18) Ta cần tìm các giá trị của v đối xứng phương trình M/N = 3x - 5: (2v^3 - 12v - 54)/(v^4 + 12v^2 + 18) = 3(t^2 - 3) - 5 (2v ^3 - 12v - 54)/(v^4 + 12v^2 + 18) = 3t^ 2 - 14 (2v^3 - 12v - 54) = (v^4 + 12v^2 + 18)(3t^2 - 14) Tuy nhiên, từ t = √(t^2 - 3), ta có v = √u = √(t^2 - 3) => (2(v^2)^3 - 12(v^2) - 54) = ((v^2)^4 + 12(v^2)^2 + 18) (3(v^2 - 3) - 14) => 2v^
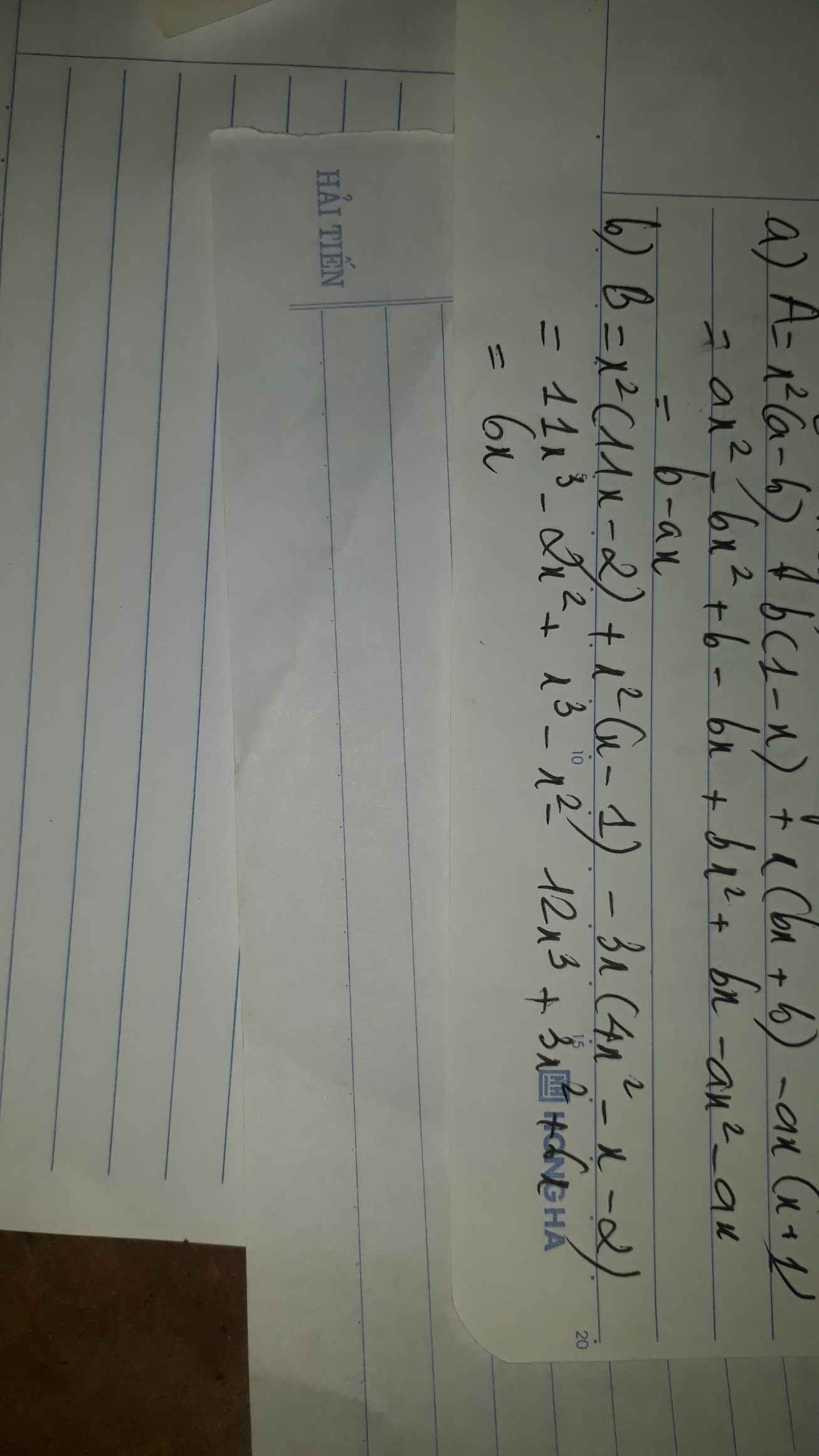
\(\Rightarrow x-3048=236\times145\\ \Rightarrow x-3048=34220\\ \Rightarrow x=34220+3048\\ \Rightarrow x=37268\)
(𝑥 − 3048): 145 = 236
𝑥 - 3048 = 236 * 145
𝑥 - 3048 = 34220
𝑥 = 34220 + 3048
𝑥 = 37268
(* là nhân)