cho tam giác đều cạnh 10cm. kẻ các đường thẳng song song với các cạnh của tam giác, các đường thẳng song song đó cách đều và cách đỉnh (căn 3)/2. tính số tam giác đều được tạo thành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 11 2018
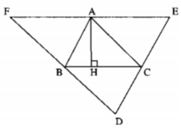
Kẻ AH ⊥ BC.
Ta có: EF // BC (gt) ⇒ AH ⊥ EF
Lại có: AE = AF (chứng minh trên)
Vậy đường cao AH là đường trung trực của EF.
Vì B là trung điểm DF và DF // AC nên đường cao kẻ từ đỉnh B của ΔABC là đường trung trực DF.
Vì C là trung điểm DE và DE // AB nên đường cao kẻ từ đỉnh C của ΔABC là đường trung trực của DE.
CM
8 tháng 3 2017
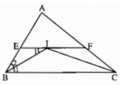
Vì điểm I cách đều ba cạnh của tam giác ABC và nằm trong tam giác nên I là giao điểm của ba đường phân giác của tam giác ABC, tức là BI, CI lần lượt là tia phân giác của góc N và góc C. Do EF // BC nên ∠B1= ∠I1(so le trong), suy ra ∠I2 = ∠B2 .
Suy ra: BI, CI lần lượt là tia phân giác của góc B và góc C.
Do EF // BC nên ∠B1 = ∠BIE (so le trong).
Lại có: ∠B1 = ∠B2 ( vì BI là tia phân giác của góc B )
Suy ra: ∠B2 = ∠BIE
Vậy EF = EI + IF = BE + CF.
HN
29 tháng 5 2017
Vì điểm I cách đều ba cạnh của tam giác ABC và nằm trong tam giác nên I là giao điểm của ba đường phân giác của tam giác ABC, tức BI, CI lần lượt là tia phân giác của góc B và góc C. Do EF // BC nên \(\widehat{B_1}=\widehat{I_1}\) (hai góc so le trong), suy ra \(\widehat{I_1}=\widehat{B_2}\). Vậy tam giác EBI cân tại E, tức là EI = EB. Tương tự ta có FI = FC.
Vậy EF = EI + IF = BE + CF.
