giúp em với
Cho hàm số y=f(x) có đạo hàm f'(x)= (x^2-1)*(x+1)*(5-x). mệnh đề nào sau đây đúng:
A. f(1)<f(4)<f(2)
B. f(1)<f(2)<f(4)
C. f(2)<f(1)<f(4)
D. f(4)<f2<f1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
f ' ( x ) = x ( x + 1 ) ( x - 2 ) 2 = 0 ⇔ [ x = 0 x = - 1 x = 2
với x=2 là nghiệm kép.
Ta có bảng biến thiên như sau:
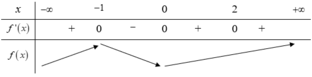
Dựa vào bảng biến thiên ta thấy hàm số đạt giá trị nhỏ nhất trên đoạn [-1;2] tại x=0.
Chọn đáp án B.

Chọn C
Trên đoạn [ - 1; 1] đồ thị hàm số y= f’( x) nằm phía trên trục hoành.
=> Trên đoạn [ - 1; 1] thì f’( x) > 0.
=> Trên đoạn [ - 1; 1] thì hàm số y= f( x) đồng biến

Đáp án A
Dựa vào bảng biến thiên ta thấy rằng ![]() .
.
![]() đổi dấu khi qua hai điểm
đổi dấu khi qua hai điểm ![]() và
và ![]() không đổi dấu khi qua điểm x=1 nên hàm số y= f(x) có hai diểm cực trị.
không đổi dấu khi qua điểm x=1 nên hàm số y= f(x) có hai diểm cực trị.
Lời giải:
\(f'(x)=(x^2-1)(x+1)(5-x)=(x+1)^2(x-1)(5-x)\)
Ta thấy \((x-1)(5-x)\geq 0, \forall x\in [1;5]\Rightarrow f'(x)=(x+1)^2(x-1)(5-x)\geq x\in [1;5]\)
Lập bảng biến thiên ta thấy hàm số đồng biến trên đoạn $[1;5]$ do đó :
\(f(1)< f(2)< f(4)\)
Đáp án B
f'(x)>=0 x thuoc [1;5]
qua du kl f(x) dong bien
=>viec Lap bang thien la viec lam thua vo bo
dap khuon robot