ĐỊNH LÝ LÁ CỜ ANH. (Cuộc thi Trí tuệ VICE - Bài viết | Facebook)
Cho một điểm P nằm trên mặt phẳng hình chữ nhất ABCD, khi đó tổng diện tích hai hình vuông với độ dài cạnh lần lượt là khoảng cách từ điểm P đến hai đỉnh đối nhau bằng tổng diện tích hai hình vuông với các cạnh lần lượt là khoảng cách từ điểm P đến hai đỉnh đối còn lại.



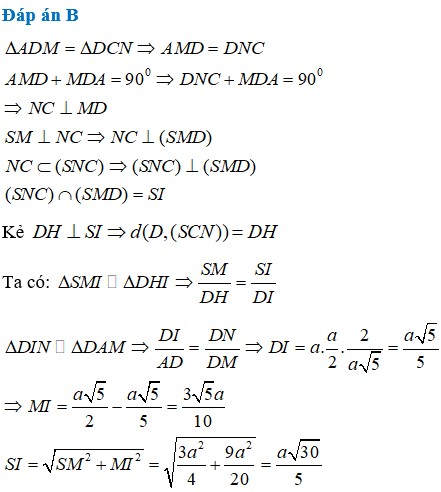
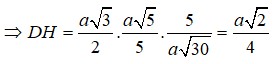

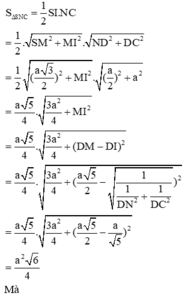
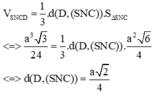

hay wóa a êi
bài vt tuyệt vời!!
Khó quá