Hai đội công nhân cùng lao động trên một công trường xây dựng. Số người đội I gấp hai lần số người đội II. Nếu chuyển 10 người từ đội I sang đội II thì số người đội II bằng 4/5 số người còn lại ở đội I . Hỏi lúc đầu mỗi đội có bao nhiêu người?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TQ
Trần Quốc Lộc
26 tháng 4 2018
Đúng(0)
Những câu hỏi liên quan
18 tháng 6 2023
Gọi số người ở đội 1,đội 2 lần lượt là a,b
Theo đề, ta có: a=2b và a-10=5/4(b+10)
=>a-2b=0 và a-5/4b=50/4+40/4=90/4
=>a=60 và b=30
17 tháng 3 2020
Gọi số người ban đầu ở đội II là x(người); số người ban đầu ở đội I là 2x (người) (x thuộc N*)
Số người sau khi chuyển ở đội II là x+10 (người)
Số người su khi chuyển ở đội I là 2x-10 (người
Vì sau khi chuyển số người ở đội II bằng \(\frac{4}{5}\)số người ở đội I nên ta có phương trình:
\(x+10=\frac{4}{5}\left(2x-10\right)\)
\(\Leftrightarrow x+10=1,6x-8\)
<=> -0,6x=-18
<=> x=30 người
=> Số người ở đội II là: 2 x 30=60 người
Vậy lúc đầu ở đội I có 30 người, đội II có 60 người
17 tháng 3 2020
Mình quên chưa ghi nguồn!
- Nguồn: Bành Thu Đạt. (h.vn)
NN
26 tháng 5 2019
Gọi số người đội 2 là x \(\left(x\inℕ^∗\right)\)
=> số người của đội 1 là 2x (người)
Nếu chuyển 10 người từ đội 1 sang đội 2 thì số người của đội 2 bằng 4/5 số người còn lại ở đội 1 nên ta có PT:
x + 10 = 4/5 (2x-10)
<=> x + 10 = 8/5. x - 8
<=> x - 8/5 .x = -8 - 10
<=> -3/5 . x = -18
<=> x = 30
Vậy số người lúc đầu của đội 2 là 30 người
Số người lúc đầu của đội 1 là: 30 . 2 = 60 người
N
26 tháng 5 2019
gọi số người đội 1 là x, số người đội 2 là y, ta có:
\(\hept{\begin{cases}2y=x\\\left(y+10\right)=\frac{4}{5}.\left(x-10\right)\end{cases}\Leftrightarrow\hept{\begin{cases}2y=x\\2y+20=\frac{8}{5}x-16\end{cases}\Leftrightarrow\hept{\begin{cases}2y=x\\2y=\frac{8}{5}x-36\end{cases}}}}\)
\(\Leftrightarrow x=\frac{8}{5}x-36\Leftrightarrow36=\frac{3}{5}x\Leftrightarrow x=60\Leftrightarrow y=\frac{60}{2}=30\)
Vậy...
21 tháng 4 2018
ssoos(. What thì sộcon số người ở đội hai làGọi số người ở đội một là x(x>10)
=> số người ở đội hai là X-2
chuyển 10 người từ đôi một sáng đôi hai thì số người ở đôi một là x-10. Số người ở đọi hai là x+10
Vì chuyện với người tự đổi mua sáu đôi hai Thế số người ở đuôi hai bằng bốn phần năm số người còn lại ở đôi một nên ta có ptrinh:4/5.(x-10)=2x+10 (=)4/5x-8=x/2+10 (=)4/5x-x/2=18 (=)8x-5x=18.10(vì mười dưới mẫu đưa lên rút x) (=)3x=180 =>x=60
vậy sổ công nhân ở đội một bằng 60
Số công nhân đọi 2 là x:2 (=)60:2=30
H
13 tháng 4 2018
Giải:
Gọi số người đội I lúc đầu là x
ĐK: \(x>10\) \((x \in N^*)\)
Số người đội II lúc đầu là \(\dfrac{1}{2}\)x
Số người đội I lúc sau là x - 10
Số người đội II lúc sau là \(\dfrac{1}{2}\)x + 10
Ta có phương trình:
\(\dfrac{1}{2}x+10=\dfrac{4}{5}\left(x-10\right)\)
\(\Leftrightarrow\dfrac{1}{2}x+10=\dfrac{4}{5}x-8\)
\(\Leftrightarrow\dfrac{1}{2}x-\dfrac{4}{5}x=-8-10\)
\(\Leftrightarrow\left(\dfrac{1}{2}-\dfrac{4}{5}\right)x=-18\)
\(\Leftrightarrow\dfrac{-3}{10}x=-18\)
\(\Leftrightarrow x=-18:\left(-\dfrac{3}{10}\right)=60\) (thỏa mãn)
Vậy ...
13 tháng 4 2018
Gọi số người ở đội II là \(x\)(người)(\(x\in N\)*)
\(\Rightarrow\) số người ở đội I là \(2x\)(người)
Theo bài ra ta có phương trình:
\(x+10=\dfrac{4}{5}\left(2x-10\right)\)
\(\Leftrightarrow x+10=\dfrac{8}{5}x-8\)
\(\Leftrightarrow\dfrac{-3}{5}x=-18\)
\(\Leftrightarrow x=30\left(TMĐK\right)\)
Vậy số người ở đội II là 30 người
\(\Rightarrow\) số người ở đội I là 2.30 = 60 người
CM
24 tháng 5 2019
Gọi x; y; z lần lượt là số người ban đầu của đội I; đội II; đội III (x, y, z ∈ N*)
Nếu chuyển 1 3 số người của đội I đi làm việc khác thì đội I còn lại 2 x 3 (người)
Nếu chuyển 1 4 số người của đội II đi làm việc khác thì đội II còn lại 3 y 4 (người)
Nếu chuyển 1 5 số người của đội III đi làm việc khác thì đội III còn lại 4 z 5 (người)
Vì số người còn lại của ba đội bằng nhau nên 2 x 3 = 3 y 4 = 4 z 5
Lại có tổng số người ban đầu của cả ba đội là 196 người nên x + y + z = 196
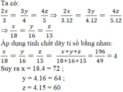
Vậy số người ban đầu của đội I, đội II, đội III lần lượt là 72, 64, 60 (người)
Đáp án cần chọn là D
1 tháng 4 2019
Gọi số người ở đội II là x(người)(x∈N*)
⇒ số người ở đội I là 2x(người)
Theo bài ra ta có phương trình:
x+10=45(2x−10)
⇔x+10=85x−8
⇔−35x=−18
⇔x=30(TMĐK)
Vậy số người ở đội II là 30 người
⇒ số người ở đội I là 2.30 = 60 người
1 tháng 4 2019
Cách 2 :
Giải:
Gọi số người đội I lúc đầu là x
ĐK: x>10 (x∈N∗)
Số người đội II lúc đầu là 12x
Số người đội I lúc sau là x - 10
Số người đội II lúc sau là 12x + 10
Ta có phương trình:
12x+10=45(x−10)
⇔12x+10=45x−8
⇔12x−45x=−8−10
⇔(12−45)x=−18
⇔−310x=−18
⇔x=−18:(−310)=60 (thỏa mãn)
Vậy ...