Cho K là điểm cách đều ba cạnh của \(\Delta MNP\) . Biết \(\widehat{MNP}\)=400 . Tính \(\widehat{MKP}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.
17 tháng 9 2023
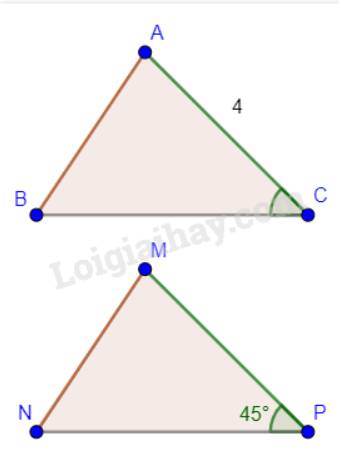
\(\Delta ABC = \Delta MNP\) nên \(AC = MP\)và \(\widehat {MPN} = \widehat {ACB}\).
Vậy \(MP = 4\)cm và \(\widehat {ACB} = 45^\circ \).
17 tháng 9 2023
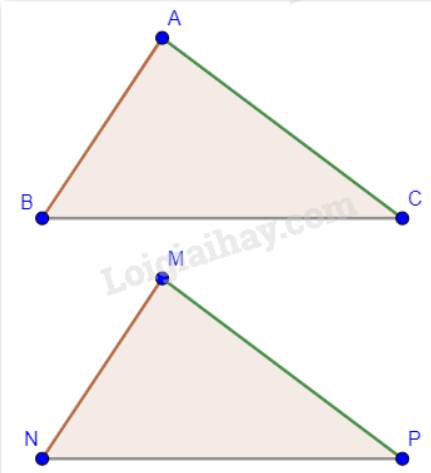
Ta có: \(\Delta ABC = \Delta MNP\) nên \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Mà \(\widehat A + \widehat N = 125^\circ \)hay \(\widehat M + \widehat N = 125^\circ \). Tổng ba góc trong một tam giác bằng 180°.
Trong tam giác MNP:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\125^\circ + \widehat P = 180^\circ \\ \to \widehat P = 180^\circ - 125^\circ = 55^\circ \end{array}\)
Vậy số đo góc P là 55°.
NT
Cho \(\Delta MNP\) \(\widehat{M}=45^0\), \(\widehat{N}=76^0\)
So sánh các cạnh của \(\Delta MNP\\ \)
1
KK
7 tháng 4 2018
xét △ MNP ta có
\(\widehat{M}+\widehat{N}+\widehat{P}=180^0\)
=> 450+760+\(\widehat{P}\) =1800
=> \(\widehat{P}=59^0\)
ta có
\(\widehat{N}>\widehat{P}>\widehat{M}\)
=> MP > MN>NP (qh góc và cạnh đối diện )
HQ
Hà Quang Minh
Giáo viên
11 tháng 1
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 50^\circ + 60^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 70^\circ \end{array}\)
Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P = 70^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g).
30 tháng 4 2023
a: Xet ΔIMN và ΔIKN có
NM=NK
góc MNI=góc KNI
NI chung
=>ΔIMN=ΔIKN
=>góc IKN=90 độ
b:Xet ΔNKA vuông tại K và ΔNMP vuông tại M có
NK=NM
góc N chung
=>ΔNKA=ΔNMP
=>NA=NP
=>ΔNAP cân tại N
mà NI là phân giác
nên NI vuông góc PA
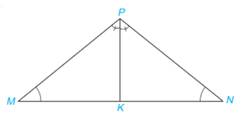
K là giao 3 đường phân giác
\(\widehat{MKP}=180^0-\dfrac{1}{2}\left(\widehat{NMP}+\widehat{MPN}\right)\)
\(\widehat{NMP}+\widehat{MPN}=180^0-\widehat{MNP}=180^0-40^0=140^0\)
\(\widehat{MKP}=180^0-\dfrac{1}{2}.140^0=110^0\)