Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
(Bạn tự vẽ hình giùm)
a/ \(\Delta BHD\)vuông và \(\Delta CKD\)vuông có: \(\widehat{B}=\widehat{C}\)(\(\Delta ABC\)cân tại A)
BD = CD (AD là đường trung tuyến của \(\Delta ABC\))
=> \(\Delta BHD\)vuông = \(\Delta CKD\)vuông (ch.gn) (đpcm)
b/ Ta có \(\Delta BHD\)= \(\Delta CKD\)(cmt) => BH = CK (hai cạnh tương ứng)
và AB = AC (\(\Delta ABC\)cân tại A)
=> AB - BH = AC - CK
=> AH = AK => \(\Delta AHK\)cân tại A (đpcm)
c/ Ta có \(\Delta AHK\)cân tại A (cmt) => \(\widehat{AHK}=\frac{180^o-\widehat{A}}{2}\)(1)
và \(\Delta ABC\)cân tại A (gt) => \(\widehat{B}=\frac{180^o-\widehat{A}}{2}\)(2)
Từ (1) và (2) => \(\widehat{AHK}=\widehat{B}\)ở vị trí đồng vị => HK // BC (đpcm)
d/ \(\Delta ADB\)và \(\Delta ADC\)có: AB = AC (\(\Delta ABC\)cân tại A)
\(\widehat{B}=\widehat{C}\)(\(\Delta ABC\)cân tại A)
BD = CD (AD là đường trung tuyến của \(\Delta ABC\))
=> \(\Delta ADB\)= \(\Delta ADC\)(c. g. c) => \(\widehat{BAD}=\widehat{CAD}\)(hai góc tương ứng) => AD là đường phân giác của \(\Delta ABC\)(đpcm)
e/ Ta có \(\Delta ADB\)= \(\Delta ADC\)(cmt) =>\(\widehat{ADB}=\widehat{ADC}\)(hai góc tương ứng)
Mà \(\widehat{ADB}+\widehat{ADC}=180^o\)(hai góc kề bù)
=> \(\widehat{ADB}=\widehat{ADC}=90^o\)=> AD \(\perp\)BC
và AD là đường trung tuyến của \(\Delta ABC\)
=> AD là đường trung trực của BC
Mà HK // BC
=> AD là đường trung trực của HK (đpcm)
a: Xet ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
=>ΔAHB=ΔAHC
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
CB chung
=>ΔNBC=ΔMCB
=>góc GBC=góc GCB
=>ΔGCB cân tại G
c: góc ECG+góc BCG=90 độ
góc GBC+góc GEC=90 độ
mà góc BCG=góc GBC
nên góc ECG=góc GEC
=>GC=GE=GB
=>G là trung điểm của BE
Xét ΔEBC có GD//CB
nên GD/CB=EG/EB=1/2
=>CB=2GD
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.
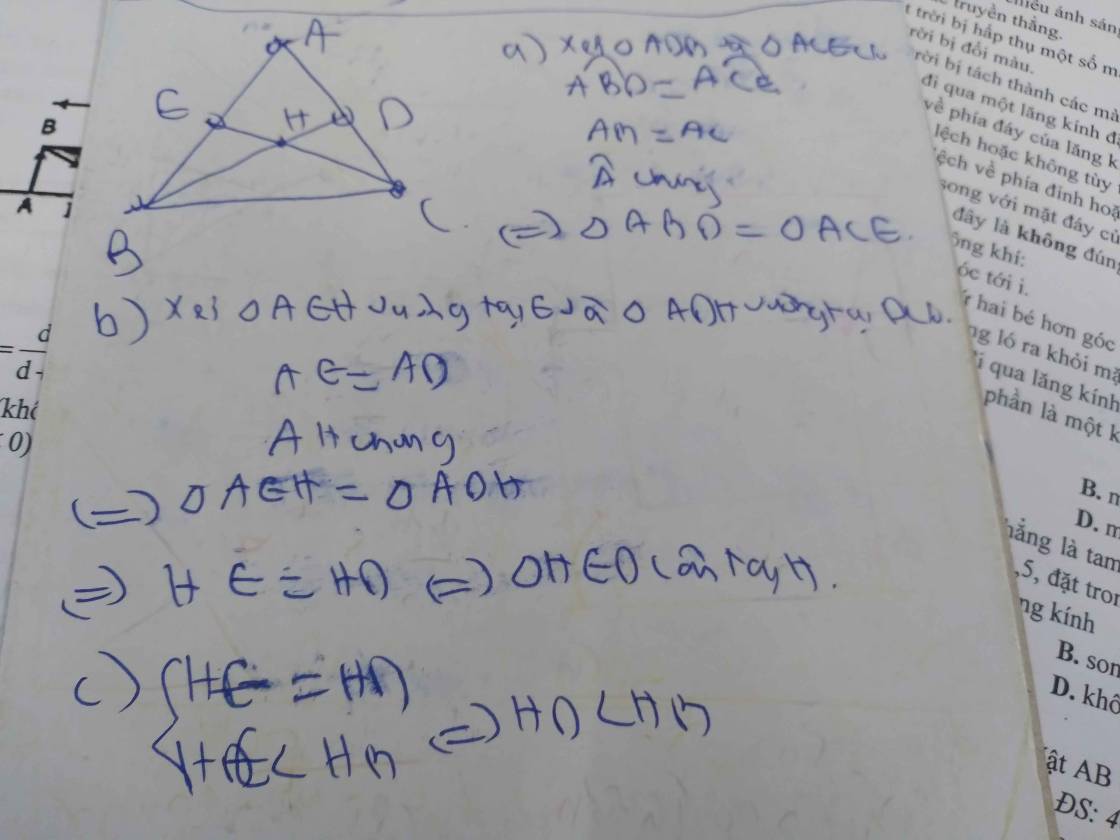
a: Xét ΔBHD vuông tại H và ΔCKD vuông tại K có
BD=CD
góc B=góc C
Do đo:ΔBHD=ΔCKD
b: Ta có: AH+HB=AB
AK+KC=AC
mà AB=AC
và BH=CK
nên AH=AK
hay ΔAHK cân tại A
c: Xét ΔABC có AH/AB=AK/AC
nên KH//BC
d: Ta có:ΔABC cân tại A
mà AD là đường trung tuyến
nen AD là phân giác của góc BAC
e: Ta có: AH=AK
DH=DK
Do dó: AD là đường trung trực của HK