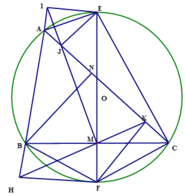
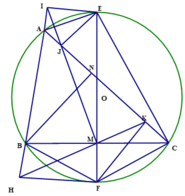
cho đường tròn tâm O bán kính R ngoại tiếp tam giác ABC có ba góc nhọn. Các tiếp tuyến của đường tròn tại các điểm B,C cắt nhau tại P. Gọi D,E là chân các đường vuông góc hạ từ P xuống AB,AC và M là trung điểm của BC
a) chứng minh \(\widehat{MEP}=\widehat{MDP}\)
b) giả sử B, C cố định và A chạy trên đường tròn (O) sao cho tam giác ABC luôn là tam giác nhọn. Chứng minh rằng đường thẳng DE luôn đi qua một điểm cố định
c)khi tam giác ABC đều, hãy tính diện tích tam giác ADE theo R