Một hình chữ nhật có diện tích 120m vuông. Tính diện tích của tứ giác có 4 đỉnh là 4 trung điểm của hình chữ nhật đã cho
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
21 tháng 4 2017
Cho hình chữ nhật ABCD; M,N,P,Q lần lượt là trung điểm của AB,BC, CD, DA.
* Chứng minh MNPQ là hình thoi
Ta có MN = PQ = 1/2BD
NP = MQ = 1/2 AC
Mà AC = BD
⇒ MN = NP = PQ = QM nên tứ giác MNPQ là hình thoi (Có 4 cạnh bằng nhau)
* Theo bài 33 (các em tham khảo ở trên), ta có SMNPQ = SABNQ và SMNPQ = SNQDC
Vì vậy SABCD = SABNQ + SNQDC = 2SMNPQ
* Ta có SABCD =2SMNPQ ⇒ SMNPQ = 1/2SABCD = 1/2AB.BC = 1/2NQ.MP
PT
21 tháng 4 2017
Vẽ hình chữ nhật ABCD với các trung điểm các cạnh M, N, P, Q.
Vẽ tứ giác MNPQ
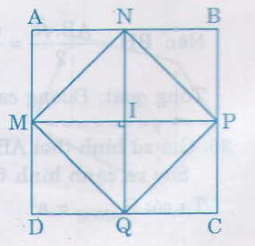
Ta có MN = PQ = \(\dfrac{1}{2}\)BD
NP = MQ = \(\dfrac{1}{2}\) AC
Mà AC = BD
Nên tứ giác MNPQ là hình thoi vì có bốn cạnh bằng nhau.
Dễ dàng chứng minh rằng : ∆AMN = ∆INM , ∆BPN = ∆NIP
∆PCQ = ∆IQP, ∆DMQ = IQM
Do đó
SMNPQ = \(\dfrac{1}{2}\) SABCD mà SABCD = AB. AD = MP. NQ
Vậy SMNPQ = \(\dfrac{1}{2}\) MP.NQ
CM
28 tháng 1 2018
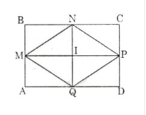
Vẽ hình chữ nhật ABCD với các trung điểm các cạnh là M, N, P, Q.
Vẽ tứ giác MNPQ
Lại có: ABCD là hình chữ nhật nên AC = BD (3)
Từ (1), (2) và (3) suy ra: MN = PQ = MQ = NP
=> Tứ giác MNPQ là hình thoi.
+ Ta có:
∆ BMN = ∆ IMN; ∆ INP = ∆ CNP, ∆ AMQ= ∆IMQ, ∆ DPQ= ∆IPQ
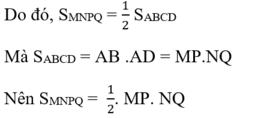
Như vậy diện tích hình thoi bằng nửa tích hai đường chéo.
CM
29 tháng 5 2018
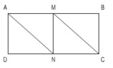
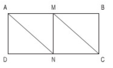
a) Hai đoạn thẳng AN và MC song song và bằng nhau vì chúng là hai cạnh đối diện của hình bình hành AMCN.
b) Diện tích hình chữ nhật ABCD là:
12 × 5 = 60 ( c m 2 )
Vì N là trung điểm của DC nên NC dài :
12 ∶ 6 = 6 cm
Diện tích hình bình hành AMCN là :
6 × 5 = 30( c m 2 )
So với diện tích hình bình hành AMCN thì diện tích hình chữ nhật ABCD gấp: 60 : 20 = 2 lần
Nói thêm : Có thể giải câu b gấp đôi đồ dài đáy hình bình hành.
Chiều rộng hình chữ nhật ABCD gắp đôi bộ dài đáy hình bình hành.
Chiều rộng hình chữ nhật ABCD bằng chiều cao hình bình hành.
Vậy diện tích hình chữ nhật gập đôi diện tích hình bình hành.
Cách 3 :
Đường gấp khúc AMNC chia hình chữ nhật ABCD thành 4 tam giác (vuông) bằng nhau. Hình bình hành AMNC gồm 2 tam giác ấy. Vậy diện tích hình chữ nhật ABCD gấp đôi diện tích hình bình hành AMCN.
CM
23 tháng 4 2018
a) Hai đoạn thẳng AN và MC song song và bằng nhau vì chúng là hai cạnh đối diện của hình bình hành AMCN.
b) Diện tích hình chữ nhật ABCD là:
12 × 5 = 60 (cm2)
Vì N là trung điểm của DC nên NC dài :
12 ∶ 2 = 6 cm
Diện tích hình bình hành AMCN là :
6 × 5 = 30(cm2)
So với diện tích hình bình hành AMCN thì diện tích hình chữ nhật ABCD gấp : 60 : 20 = 2 lần
Nói thêm : Có thể giải câu b gấp đôi đồ dài đáy hình bình hành.
Chiều rộng hình chữ nhật ABCD gắp đôi bộ dài đáy hình bình hành.
Chiều rộng hình chữ nhật ABCD bằng chiều cao hình bình hành.
Vậy diện tích hình chữ nhật gập đôi diện tích hình bình hành.
Cách 3 :
Đường gấp khúc AMNC chia hình chữ nhật ABCD thành 4 tam giác ( vuông) bằng nhau. Hình bình hành AMNC gồm 2 tam giác ấy. Vậy diện tích hình chữ nhật ABCD gấp đôi diện tích hình bình hành AMCN.
7 tháng 2 2018
diện tích hình CN là 60 xăng ti mét vuông diện tích hình bình hành là 30 xăng ti mét vuông và gấp 2 lần
14 tháng 7 2017
Ta có: * \(\frac{S_{\Delta ADE}}{S_{\Delta ADB}}=\frac{1}{2}\) mà \(\frac{S_{\Delta ADB}}{S_{ABCD}}=\frac{1}{2}\) suy ra \(\frac{S_{\Delta ADE}}{S_{ABCD}}=\frac{1}{4}\)
* \(\frac{S_{\Delta DCM}}{S_{\Delta DCB}}=\frac{1}{2}\) mà \(\frac{S_{\Delta CDB}}{S_{ABCD}}=\frac{1}{2}\) suy ra \(\frac{S_{\Delta DCM}}{S_{ABCD}}=\frac{1}{4}\)
* \(\frac{S_{\Delta EBM}}{S_{\Delta EBC}}=\frac{1}{2}\) mà \(\frac{S_{\Delta EBC}}{S_{\Delta ABC}}=\frac{1}{2}\) suy ra \(\frac{S_{\Delta EBM}}{S_{\Delta ABC}}=\frac{1}{4}\)
tuy nhiên \(\frac{S_{\Delta EBC}}{S_{ABCD}}=\frac{1}{4}\) suy ra \(\frac{S_{\Delta EBM}}{S_{ABCM}}=\frac{1}{8}\)
Ta lại có: \(\frac{S_{\Delta DEM}}{S_{ABCD}}=S_{ABCD}-\left(S_{\Delta ADE}+S_{\Delta EBM}+S_{\Delta DCM}\right)=1-\left(\frac{1}{4}+\frac{1}{4}+\frac{1}{8}\right)=\frac{3}{8}\)
\(\Rightarrow\) \(S_{ABCD}=S_{\Delta DEM}\div\frac{3}{8}=6\times\frac{8}{3}=16\left(cm^2\right)\)