1) Cho tam giác ABC vuông tại A , đường trung trực của BC cắt AC và BC theo thứ tự ở D và E
a) C/m 2CE^2 = CA.CD
b) Cho AB = 24cm , BC = 40cm. Tính các độ dài ED,CD,DA
2) Cho tam giác ABC vuông tại A , BC= 25cm , đường cao AH = 10cm. Gọi D,E theo thứ tự là chân các đường vuông góc kẻ từ H đến AB , AC
a) C/m tam giác EHA đồng dạng với tam giác ACB , tam giác ADE đồng dạng với tam giác ACB
b) Tính diện tích tam giác ADE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔCED vuông tại E và ΔCAB vuong tại A có
góc C chung
Do đó;ΔCED dồngd ạng với ΔCAB
Suy ra: CE/CA=CD/CB
=>\(CE\cdot CB=CA\cdot CD=2\cdot CE^2\)
b: CE=BC/2=20cm
AC=32cm
Ta có: ΔCED đòng dạng với ΔCAB
nên CE/CA=CD/CB=ED/AB
=>CD/40=ED/24=20/32=5/8
=>CD=25cm; ED=15cm
=>DA=7cm

Xét tam giác vuông ABC, ta có:
BC2 = AB2+ AC2 ( theo định lý py-ta-go)
BC2 = 242+ 322
BC2 = 1600
BC = 40(cm)
EC = BC : 2 = 40 : 2 = 20(cm)
Xét tam giác vuông ACB và tam giác vuông ECD có:
Có \(\widehat{A}\) = \(\widehat{E}\) = 90o
\(\widehat{C}\) chung
=> Tam giác ACB = tam giác ECD (g.g)
=> AC/EC = AB/DE
=> DE = AB.EC/AC = 15cm
Vậy DE = 15cm

Xét hai tam giác vuông ABC và MDC, ta có:
∠ (BAC) = ∠ (DMC ) = 90 0
∠ C chung
Suy ra tam giác ABC đồng dạng với tam giác MDC (g.g)
Suy ra: 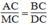
Suy ra: 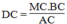
Ta có: MC = 1/2 .BC = 1/2 .24 = 12 (cm)
Vây DC = (12.24)/9 = 32 (cm)

1: \(BC=\sqrt{18^2+24^2}=30\left(cm\right)\)
2: Xét ΔABC vuông tại A và ΔIEC vuông tại I có
góc C chung
=>ΔABC đồng dạng với ΔIEC
b:
IC=BC/2=15cm
ΔABC đồng dạng với ΔIEC
=>AB/IE=BC/EC=AC/IC
=>18/IE=30/EC=24/15=8/5
=>IE=11,25cm; EC=18,75cm

1: \(BC=\sqrt{18^2+24^2}=30\left(cm\right)\)
2: Xét ΔABC vuông tại A và ΔIEC vuông tại I có
góc C chung
=>ΔABC đồng dạng với ΔIEC
b:
IC=BC/2=15cm
ΔABC đồng dạng với ΔIEC
=>AB/IE=BC/EC=AC/IC
=>18/IE=30/EC=24/15=8/5
=>IE=11,25cm; EC=18,75cm

a, Xét △ABC vuông tại A và △MDC vuông tại M
Có: ∠ACB là góc chung
=> △ABC ᔕ △MDC (g.g)
b, Xét △ABC vuông tại A có: AB2 + AC2 = BC2 (định lý Pytago)
=> 362 + 482 = BC2 => BC2 = 3600 => BC = 60 (cm)
Vì M là trung điểm BC (gt) => MB = MC = BC : 2 = 60 : 2 = 30 (cm)
Vì △ABC ᔕ △MDC (cmt) \(\Rightarrow\frac{AB}{MD}=\frac{AC}{MC}\) \(\Rightarrow\frac{36}{MD}=\frac{48}{30}\)\(\Rightarrow MD=\frac{36.30}{48}=22,5\) (cm)
và \(\frac{AC}{MC}=\frac{BC}{DC}\)\(\Rightarrow\frac{48}{30}=\frac{60}{DC}\)\(\Rightarrow DC=\frac{30.60}{48}=37,5\) (cm)
c, Xét △BME vuông tại M và △BAC vuông tại A
Có: ∠MBE là góc chung
=> △BME ᔕ △BAC (g.g)
\(\Rightarrow\frac{BM}{AB}=\frac{BE}{BC}\) \(\Rightarrow\frac{30}{36}=\frac{BE}{60}\)\(\Rightarrow BE=\frac{30.60}{36}=50\) (cm)
Vì M là trung điểm BC (gt) mà ME ⊥ BC (gt)
=> ME là đường trung trực BC
=> EC = BE
Mà BE = 50 (cm)
=> EC = 50 (cm)
e, Ta có: \(\frac{S_{\text{△}MDC}}{S_{\text{△}ABC}}=\frac{\frac{1}{2}.MD.MC}{\frac{1}{2}.AB.AC}=\frac{22,5.30}{36.48}=\frac{675}{1728}=\frac{25}{64}\)
P/s: Sao nhiều câu cùng tính EC vậy? Pls, không làm loãng câu hỏi
Bài làm
@Mấy bạn bên dưới: nghiêm cấm không trả lời linh tinh, nhất bạn luffy toán học, bạn rảnh đến nỗi cũng hùa theo họ mà spam linh tinh à.
a) Xét tam giác ABC và tam giác MDC có:
\(\widehat{BAC}=\widehat{DMC}=90^0\)
\(\widehat{BCA}\)chung
=> Tam giác ABC ~ tam giác MDC ( g - g )
b) Xét tam giác ABC vuông tại A có:
Theo pytago có:
BC2 = AB2 + AC2
hay BC2 = 362 + 482
hay BC2 = 1296 + 2304
=> BC2 = 3600
=> BC = 60 ( cm )
Mà M là trung điểm BC
=> BM = MC = BC/2 = 60/2 = 30 ( cm )
Vì tam giác ABC ~ tam giác MDC ( cmt )
=> \(\frac{AB}{MD}=\frac{BC}{DC}=\frac{AC}{MC}\)
hay \(\frac{36}{MD}=\frac{60}{DC}=\frac{48}{30}\)
=> \(MD=\frac{36.30}{48}=22,5\left(cm\right)\)
=> \(DC=\frac{60.30}{48}=37,5\left(cm\right)\)
c) Xét tam giác MBE và tam giác ABC có:
\(\widehat{BME}=\widehat{BAC}=90^0\)
\(\widehat{ABC}\)chung
=> Tam giác MBE ~ tam giác ABC ( g - g )
=> \(\frac{ME}{AC}=\frac{BM}{AB}\)
hay \(\frac{ME}{48}=\frac{30}{36}\Rightarrow ME=\frac{48.30}{36}=40\left(cm\right)\)
Xét tam giác MEC vuông tại M có:
EC2 = MC2 + ME2
hay EC2 = 302 + 402
=> EC2 = 900 + 1600
=> EC2 = 50 ( cm )
a) Vì tam giác MDC ~ Tam giác ABC
=> \(\frac{S_{\Delta MDC}}{S_{\Delta ABC}}=\left(\frac{MD}{AB}\right)^2=\left(\frac{22,5}{36}\right)^2=\left(\frac{5}{8}\right)^2=\frac{25}{36}\)
Câu c, d và câu đ giống nhau ?
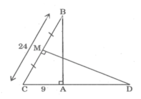
Bài 1:
a: Xét ΔCED vuông tai E và ΔCAB vuông tại A có
góc C chung
Do đo: ΔCED\(\sim\)ΔCAB
Suy ra: CE/CA=CD/CB
hay \(CA\cdot CD=CE\cdot CB=2CE^2\)
b: EC=BC/2=20(cm)
Ta có: CE/CA=CD/CB
nên 20/32=CD/40
=>CD/40=5/8
=>CD=25(cm)
AD=AC-CD=32-25=7(cm)