Cho tam giác đều ABC và M bất kì trong tam giác đó. Đ ường thẳng qua M vuông góc với BC tại H, đường thẳng qua M vuông góc với AC tại K.Đường thẳng qua M vuông góc với AB tại T. C hứng minh MH+MK+MT không phụ thuộc vị trí M.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


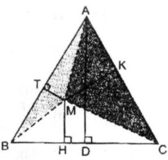
Giả sử ΔABC đều có cạnh bằng a, kẻ đường cao AD, đặt AD = h không đổi.
Ta có:
S A B C = 1/2 ah
S M A B = 1/2 MT.a
S M A C = 1/2 MK.a
S M B C = 1/2 MH.a
S A B C = S M A B + S M A C + S M B C
1/2 a.h = 1/2 MT.a + 1/2 MK.a + 1/2 MH.a
1/2 a. (MT + MK + MH)
⇒ MT + MK + MH = h không đổi
Vậy tổng MT + MK + MH không phụ thuộc vào điểm M.

Ta có:
K trọng tâm của tam giác đều ABC
=>MH=1/3AG
MK=1/3AG
MI=1/3AG
=>MI+MK+MH=AG
nha bạn chúc bạn học tốt

a) Xét ΔAMB và ΔAMC ta có:
AB = AC (gt) (1)
góc BAM = góc CAM (gt) (2)
AM là cạnh chung (3)
Từ (1),(2),(3) ⇒ΔAMB=ΔAMC (C-G-C)
b) *Xét hai tam giác vuông AHM và AKM ta có:
AM là cạnh huyền chung (3)
góc BAM = góc CAM (gt) (2)
Vậy ΔAHM=ΔAKM (cạnh huyền-góc nhọn) (4)
* Từ (4) ⇒AH=AK⇒ (2 cạnh tương ứng)

a: Xét ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔAMB=ΔAMC
b: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: AH=AK
c: Ta có: ΔAHM=ΔAKM
nên MH=MK
Ta có: AH=AK
nên A nằm trên đường trung trực của HK(1)
Ta có: MH=MK
nên M nằm trên đường trung trực của HK(2)
Từ (1) và (2) suy ra AM là đường trung trực của HK
hay AM\(\perp\)MK

 c, Chứng minh
c, Chứng minh