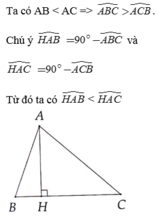
cho tam giác ABC, có ba góc nhọn, AB<AC. kẻ các đường cao AD,BE,CF cắt nhau tại H.
a) chứng minh: góc BAD bằng góc FEB
b) chứng minh: DA là phân giác của góc EDF, từ đó suy ra H cách đều EF,FD, ED
c) gọi S là giao điểm AD vả EF, chứng minh:tích của SH và AD bằng tích của AS và HD
d) gọi J,M lần lượt là trung điểm AH, BH , chứng minh JE,MD cùng cách đều một điểm