 chỉ cần chọn đáp án thui ko cần sửa đâu
chỉ cần chọn đáp án thui ko cần sửa đâu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Δ=(3m+1)^2-4(2m^2+m-1)
=9m^2+6m+1-8m^2-4m+4
=m^2+2m+5=(m+1)^2+4>=4
Do đó: PT luôn có hai nghiệm pb
b: A=(x1+x2)^2-5x2x1
=(3m+1)^2-5(2m^2+m-1)
=9m^2+6m+1-10m^2-5m+5
=-m^2+m+6
=-(m^2-m-6)
=-(m^2-m+1/4-25/4)
=-(m-1/2)^2+25/4<=25/4
Dấu = xảy ra khi m=1/2


Chiều cao là:\(14\times3=42\left(cm\right)\)
S tam giác là: \(14\times42:2=294\left(cm^2\right)\)


Số lượng số có ba chữ số là:
(999-100) : 1 + 1 = 900 (số)
Để có những số thỏa mãn điều kiện chia hết cho 2 nhưng không chia hết cho 5 => cần những số có đuôi là 2,4,6,8
Số lượng số có ba chữ số chia hết cho 2 là:
(998-100) : 2 + 1 = 450 (số)
Từ 100-999 có số lượng số tận cùng là 0 là:
(990-100) : 10 + 1 = 90 (số)
Số lượng số có 3 chữ số chia hết cho 2 nhưng không chia hết cho 5 là:
450 - 90 = 360 (số)
Vậy có 360 số thỏa mãn điều kiện đề bài.

Đặt B = \(\frac{3}{1.8}+\frac{3}{8.15}+...+\frac{3}{106.113}\)
\(\frac{7}{3}B=\frac{7}{1.8}+\frac{7}{8.15}+...+\frac{7}{106.113}\)
\(\frac{7}{3}B=1-\frac{1}{8}+\frac{1}{8}-\frac{1}{15}+....+\frac{1}{106}-\frac{1}{113}\)
\(\frac{7}{3}B=1-\frac{1}{113}=\frac{112}{113}\)
\(B=\frac{48}{113}\)
Đặt \(C=\frac{25}{50.55}+\frac{25}{55.60}+...+\frac{25}{95.100}\)
\(\frac{1}{5}C=\frac{5}{50.55}+\frac{5}{55.60}+....+\frac{5}{95.100}\)
\(\frac{1}{5}C=\frac{1}{50}-\frac{1}{55}+\frac{1}{55}-\frac{1}{60}+....+\frac{1}{95}-\frac{1}{100}\)
\(\frac{1}{5}C=\frac{1}{50}-\frac{1}{100}=\frac{1}{100}\)
\(C=\frac{1}{20}\)
\(\Rightarrow A=\frac{48}{113}-\frac{1}{20}=\frac{847}{2260}\)
HT






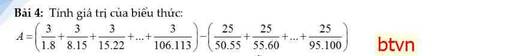
1. a
2. b
3. c
4. b
5. d
6. a
7. c
8. c
9. c
10. c
1. A
2. C
3. C
4. B
5. D
6. A
7. C
8. A
9. C
10. D