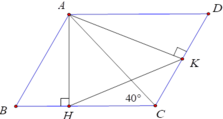
Cho tam giác ABC có góc C=40 độ .Vẽ hình bình hành ABCD. Gọi AH,AK lần lượt là các đươngcao của tam giác ABC và ACD. CMR:
a)ΔAKH đồng dạng với ΔACB.
b)Tính số đo góc AKH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
27 tháng 1 2022
a) - Ta có: SABCD=AH.BC=AK.AB.
=>\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\)
- Ta có: \(\widehat{ABC}+\widehat{BAD}=180^0\) (AD//BC).
=>\(\widehat{ABC}+\widehat{BAH}+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(90^0+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(\widehat{HAK}+\widehat{KAD}=90^0\) mà \(\widehat{KAD}+\widehat{ADK}=90^0\) (tam giác ADK vuông tại K) nên \(\widehat{HAK}=\widehat{ADK}\) mà \(\widehat{ADK}=\widehat{ABC}\) (ABCD là hình bình hành) nên\(\widehat{HAK}=\widehat{ABC}\)
- Xét tam giác AKH và tam giác BCA có:
\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\) (cmt)
\(\widehat{HAK}=\widehat{ABC}\) (cmt)
=> Tam giác AKH ∼ Tam giác BCA (c-g-c).
b) - Ta có: Tam giác AKH ∼ Tam giác BCA (cmt) nên:
\(\widehat{AKH}=\widehat{ACB}=40^0\) (2 góc tương ứng)
CM
19 tháng 1 2018
Vì AD.AH = AB.AK ( = S A B C D ) nên A H A K = A B A D = A B B C
Ta lại có AB // CD (vì ABCD là hình bình hành) mà AK ⊥ DC => AK ⊥ AB
=> BAK = 90 ∘ .
Từ đó góc HAK = ABC (cùng phụ với BAH)
Nên ΔAKH ~ ΔBCA (c.g.c) ⇒ A K H ^ = A C B ^ = 40 ∘
Đáp án: B
6 tháng 11 2021
a, \(BC=BH+HC=10\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}AH=\sqrt{BH\cdot HC}=4,8\left(cm\right)\\AB=\sqrt{BH\cdot BC}=6\left(cm\right)\end{matrix}\right.\)
\(\sin HCA=\dfrac{AB}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{HCA}\approx37^0\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 4 2023
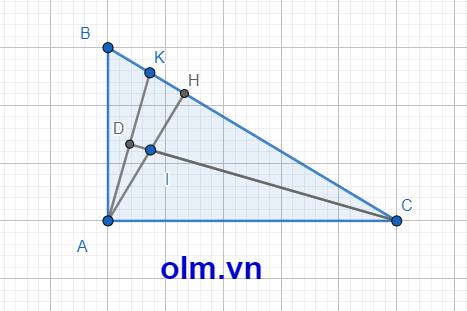
Xét \(\Delta\) HBA và \(\Delta\) ABC có \(\widehat{H}\) = \(\widehat{A}\) = 900; \(\widehat{B}\) chung
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) ABC (g-g)
Tương tự ta có: \(\Delta\) HAC \(\sim\) \(\Delta\) ABC (g-g-g)
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) HAC ( t/c hai tam giác đồng dạng)
⇒ \(\dfrac{HB}{HA}\) = \(\dfrac{HA}{HC}\) = \(\dfrac{BA}{AC}\)( theo khái niệm của tam giác đồng dạng.)
Mặt khác: KI là đường trung bình của tam giác ABH nên:
\(\dfrac{HI}{HA}\) = \(\dfrac{HK}{HB}\) ⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HB}{HA}\)
⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HA}{HC}\) mà \(\widehat{AHK}\) = \(\widehat{CHI}\) = 900
⇒ \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ( c-g-c)
b, Kéo dài CI cắt AK tại D ta có:
vì \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ⇒ \(\widehat{HAK}\) = \(\widehat{HCI}\)
Xét \(\Delta\) HAK và \(\Delta\) DCK có: \(\widehat{A}\) = \(\widehat{C}\) ( cmt)
\(\widehat{K}\) chung
⇒ \(\Delta\) HAK \(\sim\) \(\Delta\) DCK ( g-g)
⇒ \(\widehat{H}\) = \(\widehat{D}\)= 900 ⇒ AK \(\perp\) CI tại D ( đpcm)
15 tháng 10 2021
b: Xét ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
hay \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN\(\sim\)ΔACB
3 tháng 12 2021
\(a,AC=\sqrt{BC^2-AB^2}=3\sqrt{3}\left(cm\right)\\ \sin B=\dfrac{AC}{BC}=\dfrac{\sqrt{3}}{2}=\sin60^0\\ \Rightarrow\widehat{B}=60^0\\ \Rightarrow\widehat{C}=30^0\)