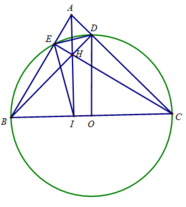
Cho tam giác ABC nhọn. Đường tròn (O) đường kính BC cắt AB,AC lần lượt tại E và D. BD cắt CE tại H;AH cắt BC tại I.Vẽ các tiếp tuyến AM và AN của (O)(M,N là các tiếp điểm).Chứng minh: a,Các tứ giác ADHE và ADIB nội tiếp đc. b,CD.CA+BE.BA=BC^2 c, M;H;N thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


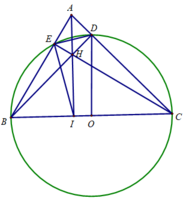
d) Tính BE.BA + CD.CA
Chứng minh tương tự câu b, CD.CA = CI.CB
Từ đó BE.BA + CD.CA = BI.BC + CI.CB
= (BI + CI).BC = BC.BC = B C 2 = 16 2 = 256

a: góc BEC=góc BDC=1/2*180=90 độ
=>CE vuông góc AB, BD vuông góc AC
góc AEH+góc ADH=180 độ
=>AEHD nội tiếp
b: góc EFH=góc ABD
góc DFH=góc ACE
mà góc ABD=góc ACE
nên góc EFH=góc DFH
=>FH là phân giác của góc EFD

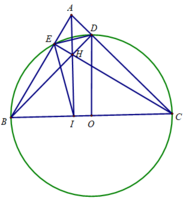
a) Chứng minh AI BC
Ta có ∠BEC = BDC = 90 0 (hai góc nội tiếp chắn nửa đườn tròn)


a: góc BEH+góc BKH=180 độ
=>BEHK nội tiếp
=>góc EBH=góc EKH
góc BKA=góc BDA=90 độ
=>ABKD nội tiếp
=>góc EBH=góc AKD=góc EKH
=>KA là phân giác của góc EKD
b: góc AIO=góc AJO=góc AKO=90 độ
=>I,J,K,A,O cùng thuộc đường tròn đường kính OA
sđ cung AI=sđ cung AJ
=>góc AKI=góc AJI
=>góc AKE+góc IKE=góc AKD+góc DKJ
=>góc IKE=góc DKJ
c:

a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: AH⊥BC
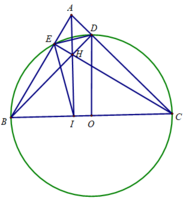
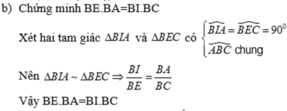

b: Xét ΔCDH vuông tại D và ΔCEA vuông tại E có
góc DCH chung
Do đó: ΔCDH\(\sim\)ΔCEA
Suy ra: CD/CE=CH/CA
hay \(CD\cdot CA=CH\cdot CE\)
Xét ΔBEH vuông tại E và ΔBDA vuông tại D có
góc EBH chung
Do đó: ΔBEH\(\sim\)ΔBDA
SUy ra: BE/BD=BH/BA
hay \(BE\cdot BA=BH\cdot BD\)
Xét ΔBIH vuông tại I và ΔBDC vuông tại D có
góc DBC chung
Do đó: ΔBIH\(\sim\)ΔBDC
Suy ra: BI/BD=BH/BC
hay \(BD\cdot BH=BI\cdot BC\)
hay \(BE\cdot BA=BI\cdot BC\)
Xét ΔCHI vuông tại I và ΔCBE vuông tại E có
góc BCE chung
Do đó: ΔCHI\(\sim\)ΔCBE
Suy ra: CH/CB=CI/CE
hay \(CH\cdot CE=CI\cdot CB\)
=>\(CI\cdot CB=CD\cdot CA\)
\(CD\cdot CA+BE\cdot BA=BI\cdot BC+CI\cdot BC=BC^2\)
a: Xét tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=180^0\)
nên ADHE là tứ giác nội tiếp
Xét tứ giác ADIB có \(\widehat{ADB}=\widehat{AIB}=90^0\)
nên ADIB là tứ giác nội tiếp