ΔA'B'C'∽ΔABC theo tỉ số đồng dạng k=\(\dfrac{2}{5}\).
a) Tính tỉ số chu vi của hai tam giác đã cho.
b) Cho biết hiệu chu vi của hai tam giác là 40dm, tính chu vi của mỗi tam giác.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ΔA'B'C' 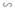 ΔA''B''C'' theo tỉ số đồng dạng k1 ⇒
ΔA''B''C'' theo tỉ số đồng dạng k1 ⇒ 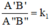
ΔA''B''C'' 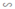 ΔABC theo tỉ số đồng dạng k2 ⇒
ΔABC theo tỉ số đồng dạng k2 ⇒ 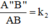
Mà ΔA'B'C' 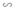 ΔA''B''C''; ΔA''B''C''
ΔA''B''C''; ΔA''B''C'' 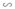 ΔABC
ΔABC
⇒ ΔA'B'C' 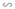 ΔABC (theo tính chất 3)
ΔABC (theo tính chất 3)
Tỉ số đồng dạng:
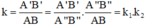
Vậy tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k1.k2.

e làm a,b chung luôn nha chị
Xét tam giác ABC và tam giác A`B`C`, có:
\(\dfrac{AB}{A`B`}=\dfrac{BC}{B`C`}=2\) ( gt )
Góc A = góc A` = 90 độ
=> tam giác ABC đồng dạng tam giác A`B`C`
=>\(\dfrac{AC}{A`C`}=\dfrac{AB}{A`B`}=\dfrac{BC}{B`C`}=2\) ( tính chất 2 tam giác đồng dạng )

Lời giải:
Giả sử $AB=3, AC=4, BC=5$ (cm)
Vì $3^2+4^2=5^2$ nên theo định lý Pitago đảo thì $ABC$ là tam giác vuông tại $A$
$A'B'C'$ đồng dạng với $ABC$ nên $A'B'C'$ là tam giác vuông tại $A'$
$\Rightarrow S_{A'B'C'}=\frac{A'B'.A'C'}{2}=54\Rightarrow A'B'.A'C'=108(*)$ (cm)
$ABC\sim A'B'C'\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}$
$\Leftrightarrow \frac{A'B'}{3}=\frac{B'C'}{5}=\frac{C'A'}{4}(**)$
Từ $(*); (**)$ suy ra $A'B'=9; B'C'=15; C'A'=12$ (cm)

Đáp án: C
Sai số tuyệt đối là: Δa = |a|.δa = 123456. 0,2% = 146,912.

Đáp án: A
Sai số tuyệt đối là: Δa = |a| . δa = 2,1739. 1% = 0,021739.

Đáp án D
+ Khi khoảng cách 2 khe tới màn là a thì tại M là vân sáng bậc 4 nên x M = 4 . λD a 2
+ Nếu lần lượt giảm hoặc tăng khoảng cách S 1 S 2 một lượng Δa thì tại đó là vân sáng bậc k và bậc 3k nên
x M = k . λD a − Δa x M = 3 k . λD a + Δa ⇒ k a − Δa = 3 k a + Δa ⇒ a = 2 . Δa
+ Nếu tăng khoảng cách S 1 S 2 thêm 2 Δa thì tại M là:
x M = k ' . λD a + 2 Δa = k ' . λD a + a = 1 2 k ' . λD a
+ So sánh với (1) ta có: x M = 1 2 k ' . λD a = 4 . λD a ⇒ k ' = 8 => Tại M khi đó là vân sáng bậc 8.
đề có sai hay nhầm chỗ nào ko bn , câu b mk tính ra số ko đẹp
Yêu cầu đúng của câu b là:
Cho biết hiệu chu vi của hai tam giác là 30cm,tính chu vi của mỗi tam giác.