Cho tam giác ABC, phân giác trong đỉnh A cắt BC tại D. Trên các đoạn thẳng DB, DC lần lượt lấy điểm E và F sao cho \(\widehat{EAD}=\widehat{FAD}\). Chứng minh rằng \(\dfrac{BE.BF}{CE.CF}\dfrac{AB^2}{AC^2}\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

25 tháng 3 2016
Kẻ EH vuông góc với AB; FK vuông góc với AB; FM vuông góc với AC; EN vuông góc với AC (H;K thuộc AB và M;N thuộc AC).
Từ D kẻ DI vuông góc với AB; DG vuông góc với AC (I thuộc AB; G thuộc AC).
-Vì HE//DI => BE/BD= HE/ID (1).
-Vì MF//DG => CF/CD= FM/DG (2).
-Từ (1);(2) => BE/CF. CD/BD= HE/ID :FM/DG= HE/FM (Do DI=DG) (3).
-Tam giác HAE đồng dạng với tam giác MAF (g.g) => HE/MF =AE/AF (4).
-Từ (3);(4) => BE/CF. CD/BD= AE/AF (5).
-Vì DI//KF => BD/BF= DI/KF (6).
-Vì DG//EN => CD/CE= DG/EN (7).
-Từ (6);(7) =>CD/CE :BD/BF= BF/CE. CD/BD= DG/EN: DI/KF= KF/EN (8).
-Tam giác KAF đồng dạng với tam giác NAE (g.g) => KF/FEN= AF/AE (9).
-Từ (8);(9) => BF/CE. CD/BD= AF/AE (10).
-Lấy (5) nhân với (10), ta có: BE/CF. CD/BD. BF/CE. CD/BD= AE/AF. AF/AE= 1.
=> BE/CE. BF/CF. (CD/BD)^2= 1. Vì AD là phân giác của góc BAC => CD/BD= AC/AB => (CD/BD)^2= (AC/AB)^2.
-Từ 2 điều trên => BE/CE. BF/CF. (AC/AB)^2= 1.
=> BE/CE. BF/CF= (AB/AC)^2 (đpcm).

13 tháng 4 2022
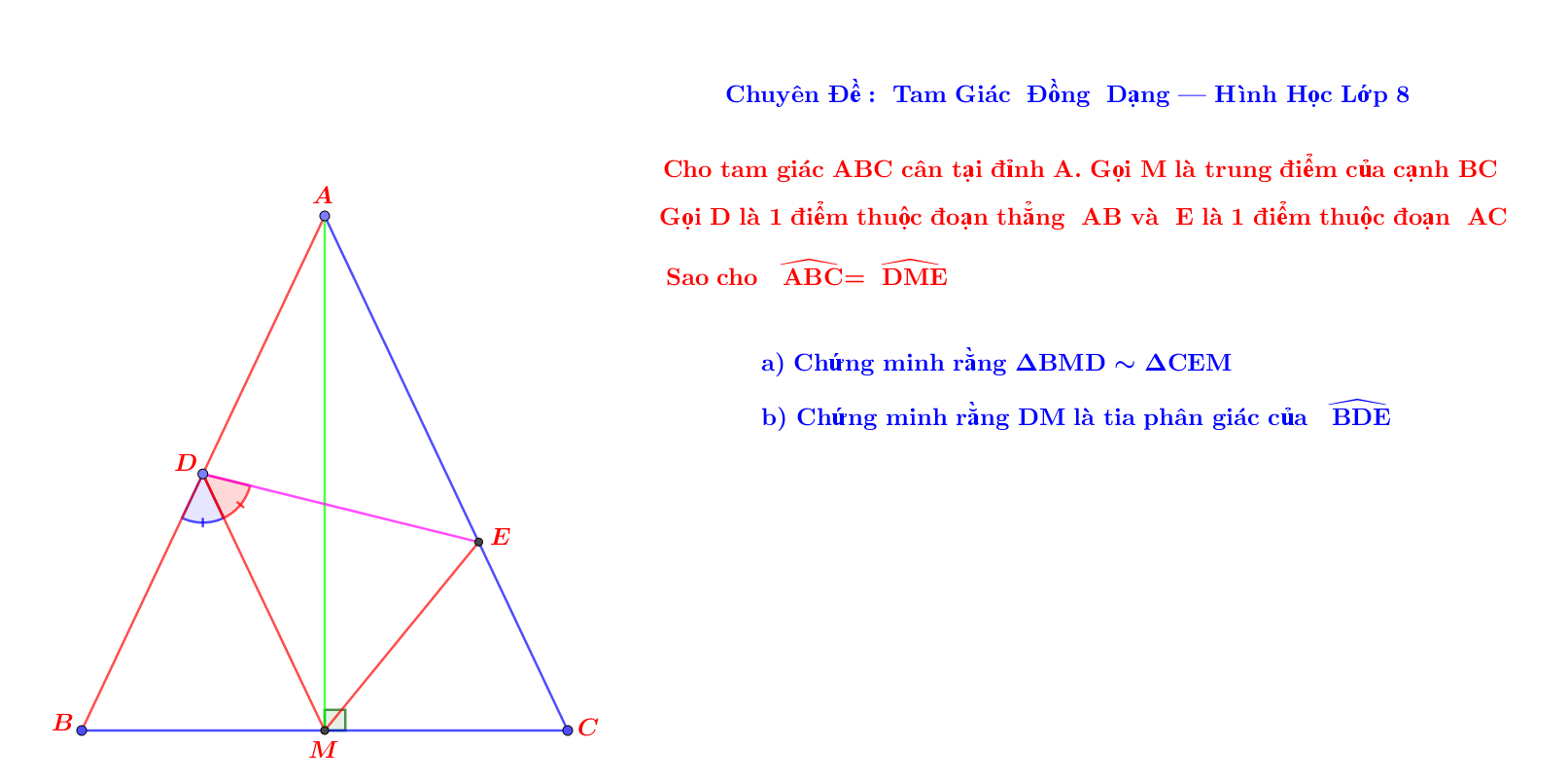
a) \(\widehat{BDM}=180^0-\widehat{BMD}-\widehat{DBM}=180^0-\widehat{BMD}-\widehat{DME}=\widehat{CME}\)
\(\Rightarrow\)△BMD∼△CEM (g-g)
b) \(\Rightarrow\dfrac{BD}{CM}=\dfrac{MD}{EM}\Rightarrow\dfrac{BD}{BM}=\dfrac{MD}{EM}\)
\(\Rightarrow\)△BMD∼△MED (c-g-c).
\(\Rightarrow\widehat{BDM}=\widehat{MDE}\Rightarrow\)DM là tia p/g góc BDE.