Cho tam giác ABC, D là điểm trên cạnh BC,E là điểm trên đoạn AD. So sánh góc ADC và góc BED; góc ADB và góc AEB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
Suy ra: DA=DE
a) Vì BD là phân giác của ABC nên ABD = CBD
Xét Δ ABD và Δ EBD có:
BA = BE (gt)
ABD = EBD (cmt)
BD là cạnh chung
Do đó, Δ ABD = Δ EBD (c.g.c)
=> AD = DE (2 cạnh tương ứng) (đpcm)
b) Δ ABD = Δ EBD (câu a) => BAD = BED = 90o (2 góc tương ứng)
=> Δ DEC vuông tại E
Δ ABC vuông tại A có: ABC + C = 90o (1)
Δ CED vuông tại E có: EDC + C = 90o (2)
Từ (1) và (2) => ABC = EDC (đpcm)
c) Gọi giao điểm của AE và BD là H
Xét Δ ABH và Δ EBH có:
AB = BE (gt)
ABH = EBH (câu a)
BH là cạnh chung
Do đó, Δ ABH = Δ EBH (c.g.c)
=> BHA = BHE (2 góc tương ứng)
Mà BHA + BHE = 180o (kề bù) nên BHA = BHE = 90o
=> BH⊥AEBH⊥AE hay BD⊥AE(đpcm)

a.
b. Xét ΔADE có góc ADE < góc AED (chứng minh ở phần a)
=> AE < AD (Quan hệ giữa góc - cạnh đối diện trong tam giác)
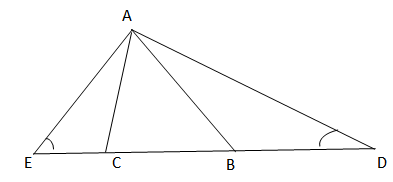
a) So sánh ˆADCADC^ và ˆAECAEC^
Ta có: AC < AB
=> ˆABC<ˆACBABC^<ACB^ (1)
Vì AC = EC => ∆AEC cân tại C
=> ˆAEC<ˆCAEAEC^<CAE^
Mà ˆACB=ˆAEC+ˆEACACB^=AEC^+EAC^ (góc ngoài tại C của ∆AEC)
=> ˆACB=2.ˆAECACB^=2.AEC^ (2)
Chứng minh tương tự : ˆABC=2ˆADCABC^=2ADC^ (3)
Từ (1), (2), (3) => 2ˆAEC=2ˆADC2AEC^=2ADC^ hay ˆAEC=ˆADCAEC^=ADC^
b) ∆AED có:
ˆAED=ˆADEAED^=ADE^ (chứng minh trên) => AD = AE

\(\widehat{EAC}=180^o-\widehat{BAC}=180^o-110^o=70^o\)
Tam giác ABC cân ở A nên \(\widehat{ACB}=\frac{180^o-\widehat{A}}{2}=\frac{180^o-110^o}{2}=35^o\) (1)
CE // AD => \(\widehat{ECD}+\widehat{ADC}=180^o\) (\trong cùng phía)
=> \(\widehat{ECD}=180^o-\widehat{ADC}=180^o-105^o=75^o\) (2)
Ta lại có: \(\widehat{ACE}=\widehat{ECD}-\widehat{ACB}=75^o-35^o=40^o\)
Trong tam giác ACE có \(\widehat{EAC}=70^o;\widehat{ACE}=40^o\)
nên góc còn lại \(\widehat{AEC}=180^o-70^o-40^o=70^o\)
Vậy tam giác ACE cân ở C và ta có:
\(70^o=\widehat{A}=\widehat{E}>\widehat{C}=40^o\)
CA = CE > AE

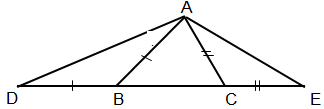

+) góc ADC là góc ngoài của tam giác BED tại đỉnh D => góc ADC > BED
+) Góc AEB là góc ngoài của tam giác BED tại đỉnh E => góc AEB > BDA