cho phương trinh : 2x2-5x+6+21-x2=26-5x .tìm tích các nghiệm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 5 2018
Chọn C.
Phương pháp: Biến đổi đưa về phương trình tích.
Cách giải:
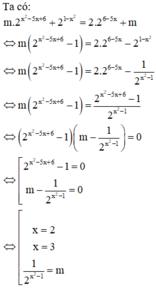
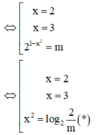
Vậy để phương trình đã cho có 4 nghiệm phân biệt thì (*) phải có 2 nghiệm phân biệt khác 2 và 3.
CM
8 tháng 5 2019
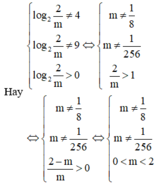
Điều kiện xác định x 2 + 5 x + 10 ≥ 0 ⇔ x ∈ R
Khi đó phương trình ⇔ x 2 + 5 x + 10 + 2 x 2 + 5 x + 10 − 8 = 0
⇔ ( x 2 + 5 x + 10 − 2 ) ( x 2 + 5 x + 10 + 4 ) = 0
⇔ x 2 + 5 x + 10 = 2 x 2 + 5 x + 10 = − 4 ⇔ x 2 + 5 x + 10 = 2 ⇔ x 2 + 5 x + 6 = 0 ⇔ x = − 3 x = − 2
Vậy x 1 2 + x 2 2 = 2 2 + 3 3 = 13
Đáp án cần chọn là: B
KK
3
11 tháng 4 2023
Phân tích đa thức thành nhân tử thôi bạn :
Ta có :
\(h\left(x\right)=x^2+5x+6\)
\(h\left(x\right)=x\left(x+2\right)+3\left(x+2\right)\)
\(h\left(x\right)=\left(x+2\right)\left(x+3\right)\)
\(\Rightarrow N_oh\left(x\right)=-2;-3\)
\(g\left(x\right)=2x^2+7x-9\)
\(g\left(x\right)=2x^2+9x-2x-9\)
\(g\left(x\right)=2x\left(x-1\right)+9\left(x-1\right)\)
\(g\left(x\right)=\left(x-1\right)\left(2x+9\right)\)
\(\Rightarrow N_og\left(x\right)=1;-4,5\)
25 tháng 5 2022
\(\Delta=\left(-5\right)^2-4\left(m-1\right)\)
\(=25-4m+4\)
\(=29-4m\)
Để pt có 2 nghiệm thì \(\Delta>0\)
\(\Leftrightarrow m< \dfrac{29}{4}\)
Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=m-1\end{matrix}\right.\) (1)
\(2x_2=\sqrt{x_1}\) ; \(ĐK:x_1;x_2\ge0\)
\(\Leftrightarrow4x_2^2=\left|x_1\right|\)
\(\Leftrightarrow4x_2^2=x_1\) (2)
Thế \(x_1=4x^2_2\) vào \(\left(1\right)\), ta được:
\(\left\{{}\begin{matrix}4x_2^2+x_2-5=0\\4x_2^3-m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x_2=-\dfrac{5}{4}\left(ktm\right)\\x_2=1\left(tm\right)\end{matrix}\right.\\4.1^3-m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=1\\m=5\end{matrix}\right.\)
\(\left(2\right)\Rightarrow x_1=4\)
Vậy \(\left\{{}\begin{matrix}m=5\\x_1=4\\x_2=1\end{matrix}\right.\)
H
9 tháng 4 2023
\(3x^2+5x-6=0\\ \Delta=5^2-4.3.\left(-6\right)=97\\ \Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-5+\sqrt{97}}{2}\\x_2=\dfrac{-5-\sqrt{97}}{2}\end{matrix}\right.\)
\(\left(x_1-2x_2\right).\left(2x_1-x_2\right)=2x^2_1-4x_1x_2+2x_2^2\)
\(=2.\left(\dfrac{-5+\sqrt{97}}{2}\right)^2-4.\left(\dfrac{-5+\sqrt{97}}{2}\right).\left(\dfrac{-5-\sqrt{97}}{2}\right)+2.\left(\dfrac{-5-\sqrt{97}}{2}\right)^2\\ =\left(\dfrac{-5+\sqrt{97}}{2}\right)^2-2.\left(\dfrac{-5+\sqrt{97}}{2}\right).\left(\dfrac{-5-\sqrt{97}}{2}\right)+\dfrac{\left(-5-\sqrt{97}\right)^2}{2^2}\\ =\left(\dfrac{-5+\sqrt{97}}{2}-\dfrac{-5-\sqrt{97}}{2}\right)^2\\ =\left(\dfrac{-5+\sqrt{97}+5+\sqrt{97}}{2}\right)^2\\ =\left(\dfrac{2\sqrt{97}}{2}\right)^2\\ =\left(\sqrt{97}\right)^2=97\)
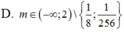
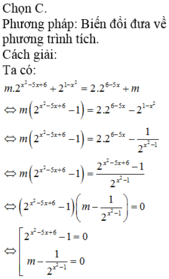
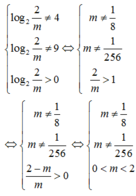
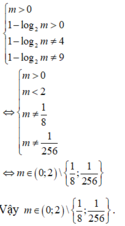
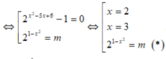
Lời giải:
Đặt \(\left\{\begin{matrix} 1-x^2=a\\ 6-5x=b\end{matrix}\right.\)
PT trở thành:
\(2^{1+b-a}+2^a=2^b\)
\(\Leftrightarrow 2^a(2^{1+b-2a}+1-2^{b-a})=0\)
\(\Leftrightarrow 2^{1+b-2a}-2^{b-a}=-1< 0\)
\(\Leftrightarrow 2^{1+b-2a}< 2^{b-a}\)
\(\Leftrightarrow 1+b-2a< b-a\Leftrightarrow 1-a< 0\Leftrightarrow 1< a\)
\(\Leftrightarrow 1-x^2> 1\Leftrightarrow x^2< 0\) (vô lý)
Do đó PT vô nghiệm.