1/2×(x2+y2)-2x2y2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\left(2x^3-x^2+5x\right):x\)
\(=\dfrac{2x^3-x^2+5x}{x}\)
\(=\dfrac{x\left(2x^2-x+5\right)}{x}\)
\(=2x^2-x+5\)
b) \(\left(3x^4-2x^3+x^2\right):\left(-2x\right)\)
\(=\dfrac{3x^4-2x^3+x^2}{-2x}\)
\(=\dfrac{2x\left(\dfrac{3}{2}x^3-x^2+\dfrac{1}{2}x\right)}{-2x}\)
\(=-\left(\dfrac{3}{2}x^3-x^2+\dfrac{1}{2}x\right)\)
\(=-\dfrac{3}{2}x^3+x^2-\dfrac{1}{2}x\)
c) \(\left(-2x^5+3x^2-4x^3\right):2x^2\)
\(=\dfrac{-2x^5+3x^2-4x^3}{2x^2}\)
\(=\dfrac{2x^2\left(-x^3+\dfrac{3}{2}-2x\right)}{2x^2}\)
\(=-x^3-2x+\dfrac{3}{2}\)
d) \(\left(x^3-2x^2y+3xy^2\right):\left(-\dfrac{1}{2}x\right)\)
\(=\dfrac{x^3-2x^2y+3xy^2}{-\dfrac{1}{2}x}\)
\(=\dfrac{\dfrac{1}{2}x\left(2x^2-4xy+6y^2\right)}{-\dfrac{1}{2}x}\)
\(=-\left(2x^2-4xy+6y^2\right)\)
\(=-2x^2+4xy-6y^2\)
e) \(\left[3\left(x-y\right)^5-2\left(x-y\right)^4+3\left(x-y\right)^2\right]:5\left(x-y\right)^2\)
\(=\dfrac{3\left(x-y\right)^5-2\left(x-y\right)^4+3\left(x-y\right)^2}{5\left(x-y\right)^2}\)
\(=\dfrac{5\left(x-y\right)^2\left[\dfrac{3}{5}\left(x-y\right)^3-\dfrac{2}{5}\left(x-y\right)^2+\dfrac{3}{5}\right]}{5\left(x-y\right)^2}\)
\(=\dfrac{3}{5}\left(x-y\right)^3-\dfrac{2}{5}\left(x-y\right)^2+\dfrac{3}{5}\)
f) \(\left(3x^5y^2+4x^3y^3-5x^2y^4\right):2x^2y^2\)
\(=\dfrac{3x^5y^2+4x^3y^3-5x^2y^4}{2x^2y^2}\)
\(=\dfrac{2x^2y^2\left(\dfrac{3}{2}x^3+2xy-\dfrac{5}{2}y^2\right)}{2x^2y^2}\)
\(=\dfrac{3}{2}x^3+2xy-\dfrac{5}{2}y^2\)

1: Phân tích thành nhân tử
c) Ta có: \(x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)+z^3-3xyz\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-z\left(x+y\right)+z^2\right]-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)\)

1: \(=\dfrac{x-1}{x^2+x+1}+\dfrac{x+1}{x-1}\)
\(=\dfrac{x^2-2x+1+x^3+x^2+x^2+x+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3+3x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}\)
2: \(=\dfrac{\left(x^2-y^2\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{\left(x-y\right)\left(x+y\right)^2}{x^2+xy+y^2}\)

Bài 1:
\(a,2x^2y\left(2x^2y^2-xy^2\right)\\ =2x^2x^2y^2y-2x^2x.y^2.y=2x^4y^3-2x^3y^3\\ b,\left(x-1\right)\left(2x+3\right)\\ =x.2x+x.3-1.2x-1.3=2x^2+3x-2x-3\\ =2x^2+x-3\\ c,\left(20x^3y^4+10x^2y^3-5xy\right):5xy\\ =20x^3y^4:5xy+10x^2y^3:5xy-5xy:5xy\\ =\left(20:5\right).\left(x^3:x\right).\left(y^4:y\right)+\left(10:5\right).\left(x^2:x\right).\left(y^3:y\right)-\left(5:5\right).\left(x:x\right).\left(y:y\right)\\ =4x^2y^3+2xy^2-1\\ d,\left(y-3x\right)^2-\left(y^2-6xy\right)\\ =\left[y^2-2.y.3x+\left(3x\right)^2\right]-\left(y^2-6xy\right)\\ =y^2-6xy+9x^2-y^2+6xy =9x^2\)
Bài 2:
\(a,4xy+4xz=4x\left(y+z\right)\\ b,x^2-y^2+9-6x\\ =\left(x^2-6x+9\right)-y^2\\ =\left(x-3\right)^2-y^2\\ =\left(x-3-y\right)\left(x-3+y\right)\)
Bài 3:
\(a,\dfrac{3xy}{y+z}+\dfrac{3xz}{y+z}\\=\dfrac{3xy+3xz}{y+z}\\ =\dfrac{3x\left(y+z\right)}{\left(y+z\right)}=3x\left(Với:y\ne-z\right)\\ b,\dfrac{x}{x+2}-\dfrac{x}{x-2}\\ =\dfrac{x\left(x-2\right)-x\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}\\ =\dfrac{x^2-2x-x^2-2x}{\left(x+2\right)\left(x-2\right)}=0\)

Bạn vui lòng viết đề đầy đủ, và gõ bằng công thức toán để được hỗ trợ tốt hơn.

\(x^2+2x^2y^2+2y^2-\left(x^2y^2+2x^2\right)-2=0\)
\(\Leftrightarrow x^2+2x^2y^2+2y^2-x^2y^2-2x^2-2=0\)
\(\Leftrightarrow x^2y^2-x^2+2y^2-2=0\)
\(\Leftrightarrow\left(x^2y^2-x^2\right)+\left(2y^2-2\right)=0\)
\(\Leftrightarrow x^2\left(y^2-1\right)+2\left(y^2-1\right)=0\)
\(\Leftrightarrow\left(x^2+2\right)\left(y^2-1\right)=0\)
\(\Leftrightarrow\left(x^2+2\right)\left(y-1\right)\left(y+1\right)=0\)
Dễ thấy: \(x^2+2\ge2>0\forall x\) (vô nghiệm)
\(\Rightarrow\left[{}\begin{matrix}y-1=0\\y+1=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=1\\y=-1\end{matrix}\right.\)
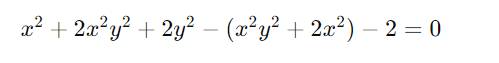
Bạn nên gõ lại cho cẩn thận,mình thấy để sai.
đề nè
1/2*(2x2+y2)-2x2y2