Tính: \(8\sqrt{2}\left(\sqrt{24+16\sqrt{2}}-\sqrt{24-16\sqrt{2}}\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\sqrt{24+16\sqrt{2}}-\sqrt{24-16\sqrt{2}}=\sqrt{\left(4+\sqrt{8}\right)^2}-\sqrt{\left(4-\sqrt{8}\right)^2}=\left|4+\sqrt{8}\right|-\left|4-\sqrt{8}\right|=4+\sqrt{8}-4+\sqrt{8}=4\sqrt{2}\)

a,ĐK: x\(\ge\)1
⇔\(\sqrt{x-1-2\sqrt{x-1}+1}\)=\(\sqrt{2}\)
⇔\(\sqrt{\left(\sqrt{x-1}-1\right)^2}\)=\(\sqrt{2}\)
⇔\(\left|\sqrt{x-1}-1\right|\)=\(\sqrt{2}\)
TH1:\(\sqrt{x-1}\)-1≥0⇒\(\left|\sqrt{x-1}-1\right|\)=\(\sqrt{x-1}\)-1 bn tự giải ra nha
TH2:\(\sqrt{x-1}\)-1<0⇒\(\left|\sqrt{x-1}-1\right|\)=1-\(\sqrt{x-1}\) bn tự lm nha

22) \(\frac{1}{\sqrt{5}+\sqrt{2}}+\frac{1}{\sqrt{5}-\sqrt{2}}\)
\(=\frac{\left(\sqrt{5}-\sqrt{2}\right)+\left(\sqrt{5}+\sqrt{2}\right)}{\left(\sqrt{5}+\sqrt{2}\right)\left(\sqrt{5}-\sqrt{2}\right)}\)
\(=\frac{2\sqrt{5}}{\sqrt{5^2}-\sqrt{2^2}}\)
\(=\frac{2\sqrt{5}}{5-2}=\frac{2\sqrt{5}}{3}\)

a,\(3\dfrac{17}{24}+\left(2\dfrac{8}{15}-4\dfrac{8}{15}\right):\left(2\dfrac{11}{30}-\dfrac{11}{30}\right)\)
\(=\dfrac{89}{24}-2:2\)
\(=\dfrac{65}{24}\)
b,\(0,5:\sqrt{625}-\sqrt{\dfrac{4}{25}}+0,18.\left(\sqrt{1\dfrac{9}{16}}-\sqrt{\dfrac{9}{16}}\right)\)
\(=0,5:25-\dfrac{2}{5}+0,18.\dfrac{1}{2}\)
\(=-\dfrac{29}{100}\)

Bài 2:
a)\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\) (đk: \(x\ge2\))
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9\left(x-2\right)}+\dfrac{6}{\sqrt{81}}\sqrt{x-2}=-4\)
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-2\sqrt{x-2}+\dfrac{2}{3}\sqrt{x-2}=-4\)
\(\Leftrightarrow-\sqrt{x-2}=-4\) \(\Leftrightarrow x-2=16\)
\(\Leftrightarrow x=18\) (thỏa)
Vậy...
b)\(\sqrt{9x^2+12x+4}=4x\)(Đk:\(9x^2+12x+4\ge0\))
\(\Leftrightarrow\left\{{}\begin{matrix}4x\ge0\\9x^2+12x+4=16x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+12x+4=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+14x-2x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x-2\right)\left(-7x-2\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=2\\x=-\dfrac{2}{7}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x=2\) (tm đk)
Vậy...
c) \(\sqrt{x-2\sqrt{x-1}}=\sqrt{x-1}\) (đk: \(x\ge1\))
\(\Leftrightarrow x-2\sqrt{x-1}=x-1\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{1}{2}\) \(\Leftrightarrow x=\dfrac{5}{4}\) (tm)
Vậy...
tính x=\(\sqrt{97-56\sqrt{3}}+\sqrt{52+16\sqrt{3}}\)
y=\(\sqrt{33+20\sqrt{2}}+\sqrt{24-16\sqrt{2}}\)

Ta có: \(x=\sqrt{97-56\sqrt{3}}+\sqrt{52+16\sqrt{3}}\)
\(=\sqrt{49-2\cdot7\cdot4\sqrt{3}+48}+\sqrt{48+2\cdot4\sqrt{3}\cdot2+4}\)
\(=\sqrt{\left(7-4\sqrt{3}\right)^2}+\sqrt{\left(4\sqrt{3}+2\right)^2}\)
\(=\left|7-4\sqrt{3}\right|+\left|4\sqrt{3}+2\right|\)
\(=7-4\sqrt{3}+4\sqrt{3}+2\)
\(=9\)
Làm luôn phần y :D
y = \(\sqrt{33+20\sqrt{2}}+\sqrt{24-16\sqrt{2}}\)
y = \(\sqrt{33+2.10\sqrt{2}}+\sqrt{24-2.8\sqrt{2}}\)
y = \(\sqrt{33+2.5.2\sqrt{2}}+\sqrt{24-2.4.2\sqrt{2}}\)
y = \(\sqrt{25+2.5.\sqrt{8}+8}+\sqrt{16-2.4.\sqrt{8}+8}\)
y = \(\sqrt{\left(5+\sqrt{8}\right)^2}+\sqrt{\left(4-\sqrt{8}\right)^2}\)
y = |5 + \(\sqrt{8}\)| + |4 - \(\sqrt{8}\)|
y = 5 + \(\sqrt{8}\) + 4 - \(\sqrt{8}\) (Vì 4 > \(\sqrt{8}\) nên 4 - \(\sqrt{8}\) > 0)
y = 9
Vậy y = 9
Chúc bn học tốt!
thực hiện phép tính:\(\sqrt{\left(5-\sqrt{24}^{ }\right)^2}\)- \(\sqrt{\left(5+\sqrt{24}\right)^2}\)

\(\sqrt{\left(5-\sqrt{24}\right)^2}-\sqrt{\left(5+\sqrt{24}\right)^2}\\ =\left|5-\sqrt{24}\right|-\left|5+\sqrt{24}\right|\\ =5-\sqrt{24}-5-\sqrt{24}\\ =-2\sqrt{24}=-4\sqrt{6}\)
`\sqrt((5-\sqrt24)^2) - \sqrt((5+\sqrt24)^2)`
`=|5-\sqrt24|-|5+\sqrt24|`
`=5-\sqrt24-5-\sqrt24`
`=-2\sqrt24`
`=-4\sqrt6`
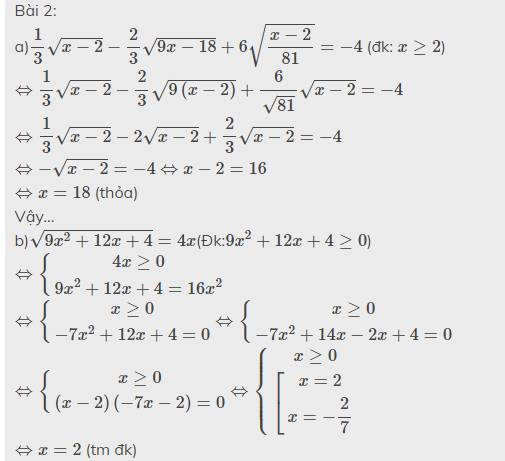
\(8\sqrt{2}\left(\sqrt{24+16\sqrt{2}}-\sqrt{24-16\sqrt{2}}\right)\)
\(=8\sqrt{2}\left(\sqrt{16+2.4.\sqrt{8}+8}-\sqrt{16-2.4\sqrt{8}+8}\right)\)
\(=8\sqrt{2}\left(\sqrt{\left(4+\sqrt{8}\right)^2}-\sqrt{\left(4-\sqrt{8}\right)^2}\right)\)
\(=8\sqrt{2}\left(4+\sqrt{8}-4+\sqrt{8}\right)\)
\(=8\sqrt{2}.2\sqrt{8}\)
= 64
ta có\(8\sqrt{2}\cdot\left(\sqrt{24+16\sqrt{2}}-\sqrt{24-16\sqrt{2}}\right)=8\sqrt{2}\cdot\left(\sqrt{\left(4+\sqrt{8}\right)^2}-\sqrt{\left(4-\sqrt{8}\right)^2}\right)=8\sqrt{2}\cdot\left(4+\sqrt{8}-4+\sqrt{8}\right)=8\sqrt{2}\cdot2\sqrt{8}=64\)vây..................