Cho hình tứ diện ABCD. Gọi M N , lần lượt là trung điểm của AB CD , .Tìm giao tuyến của các cặp mặt phẳng sau : 1. (ABN )và ( ACD ) 2. ( ABN ) và( CDM )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


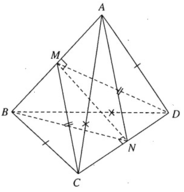
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó MN ⊥ CD vì N là trung điểm của CD. Tương tự ta chứng minh được NA = NB và suy ra MN ⊥ AB. Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.

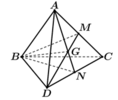
Ta có B là điểm chung thứ nhất.
Gọi 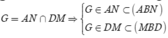
=> G là điểm chung thứ hai.
Vậy ![]()
Chọn C.

a: \(N\in SC\subset\left(SCD\right)\)
\(N\in\left(ABN\right)\)
Do đó: \(N\in\left(SCD\right)\cap\left(ABN\right)\)
Xét (SCD) và (ABN) có
\(N\in\left(SCD\right)\cap\left(ABN\right)\)
CD//AB
Do đó: (SCD) giao (ABN)=xy, xy đi qua N và xy//AB//CD
c: Chọn mp(SAC) có chứa AN
Gọi O là giao điểm của AC và BD trong mp(ABCD)
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi K là giao điểm của AN với SO
=>K là giao điểm của AN với mp(SBD)


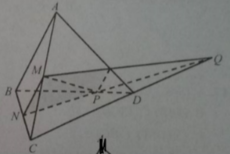
a, Do N là trung điểm của CD ⇒ N ∈ (ACD).
Ta có N ∈ (ABN).
Mặt khác: A ∈ (ACD) và A ∈ (ABN)
⇒ (ACD) \(\cap\) (ABN) = AN
b, Do N ∈ CD ⇒ N ∈ (CDM). Hiển nhiên : N ∈ (ABN)
Do M ∈ AB nên M ∈ (ABN). Hiển nhiên : M ∈ (CDM)
⇒ (ABN) \(\cap\) (CDM) = MN