Cho bieu thuc u=120 căn 2 cos pi t cuốn cảm có điện dung 200 pi m h dien trở 30 ôm mắc nối tiêp . Cho biet giá trị cuc đại cua dien ap gia trị hieu dung cua dien ap lan so goc chu ki pha ban dau pha dao dong. Tinh cường đô dòng dien trong mạch
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


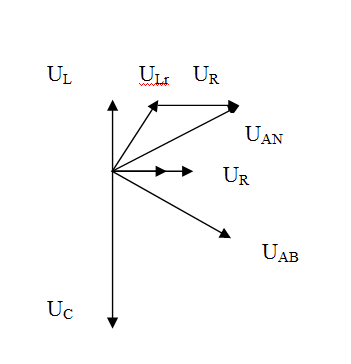
Ta có: \(U_{AB}=U_{AN}=\sqrt{3}U_{MN}=120V\) \(U_R=120V\) \(U_{AB}=U_{AN}\) do đó \(Z_L=U_{LC}\) hay góc hợp giữa \(U_{AB}\) và I bằng góc hợp bởi \(U_{AN}\) và I (cùng có R và r) Mặt khác theo đầu bài của các góc bằng nhau ta suy ra được \(\overrightarrow{U_{AN}}\) là phân giác của góc hợp bởi \(U_{Lr}\) và I \(\overrightarrow{U_{AN}}=\overrightarrow{U_{Lr}}+\overrightarrow{U_R}\) Xét tam giác đã tịnh tiến \(\overrightarrow{U_R}\) lên trên thì theo góc so le của 2 đường song song suy ra đây là tam giác cân \(U_{Lr}=U_R=120V\) Từ đó suy ra góc nhỏ trong tam giác bằng \(\pi\text{ /}6\) Do đó \(U_L=60\sqrt{3}V\) \(Z_L=\frac{U_L}{I}=15\sqrt{6}\Omega\)
|

Bài chỉ có 1 tụ điện nên cường độ dòng điện nhanh pha hơn hiệu điện thế \(\text{π/2}\)
Giả sử phương trình của cường độ dòng điện là
\(i=I_0\cos\left(u\right)\)
Thì phương trình của hiện điện thế 2 đầu đoạn mạch là
\(u=U_0\cos\left(u-\text{π/2}\right)=U_0\sin\left(u\right)\)
Ta có
\(\frac{u^2}{U^2_0}+\frac{i^2}{I^2_0}=\sin^2u+\cos^2u=1\)
Đây là phương trình của elip

\(Z_L=\omega L=100\Omega\)
Ta áp dụng một tính chất của mạch RLC khi C thay đổi để Uc max là lúc đó u mạch vuông pha với uRL.
Như vậy, bài này theo giả thiết uAB lệch pha pi/2 so với uAM là thỏa mãn điều kiện trên.
=> \(Z_C=\frac{R^2+Z_L^2}{Z_L}=\frac{50^2+100^2}{100}=125\Omega\)
=> C

Bạn vẽ giản đồ véc tơ sẽ suy ra đc \(Z_d=30\Omega\)
\(\Rightarrow r=Z_d\cos 60^0=15\Omega\)
Vậy điện trở hoạt động của mạch
\(R+r=45\Omega\)

\(Z_L=40\Omega\)
\(U_L=IZ_L=\frac{U}{Z}Z_L=\frac{120.40}{\sqrt{30^2+\left(40-Z_C\right)^2}}\)
Suy ra \(U_L\)max khi \(Z_C=40\Omega\)
\(U_{Lmax}=\frac{120.40}{30}=160V\)