Một hợp chất ion được cấu tạo từ \(M^+\) và \(X^{2-}\).Trong phần tử \(M_2X\) có tổng số hạt proton,nơtron,electron là 140 hạt.Trong đó số hạt mang điện nhiều hơn số hạt không mang điện là 44 hạt.Số khối của ion \(M^+\) lớn hơn số khối của ion \(X^{2-}\) là 23.Tổng số hạt proton,nơtron,electron trong ion \(M^+\) nhiều hơn trong ion \(X^{2-}\) là 31.Viết cấu hình electron của M và X
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Gọi p, e, n là số proton, số electron và số nơtron trong một nguyên tử M; p’, e’, n’ là số proton, số electron và số nơtron trong một nguyên tử X.
Trong nguyên tử số proton = số electron; các hạt mang điện là proton và electron, hạt không mang điện là nơtron.
+ Trong phân tử của M2X2 có tổng số hạt proton, nơtron và electron là 164 nên suy ra:
2(2p + n) + 2(2p’ + n’) = 164 (1)
+ Trong đó số hạt mang điện nhiều hơn hạt không mang điện là 52 nên suy ra:
(4p + 4p’) - 2(n + n’) = 52 (2)
+ Số khối của M lớn hơn số khối của X là 23 đơn vị nên ta có suy ra:
(p + n) - (p’ + n’) = 23 (3)
+ Tổng số hạt electron trong M+ nhiều hơn trong X22- là 7 hạt nên suy ra:
(2p + n - 1) - 2(2p’ + n’) + 2 = 7 (4)
Giải hệ (1), (2), (3), (4) ta được p = 19 ⇒ M là kali; p’ = 8 ⇒ X là oxi.
Công thức phân tử của hợp chất là K2O2.

Đáp án B
Gọi a, b là lần lượt tổng số proton và nơtron
Ta có: 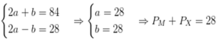
Ta có:
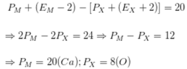
M là canxi ở ô 20, chu kì 4, nhóm IIA
Chọn B

Đáp án : A
A là M2X :
2.(2pM + nM) + (2pX + nX) = 140(1)
Số hạt mang điện trong M+ = 2pM – 1
Số hạt mang điện trong X2- = 2pX + 2
=> 2pM – 1 = (2pX + 2) + 19
=> pM – pX = 11(2)
Trong M : pM + 1 = nM(3)
Trong X : pX = nX (4)
Giải hệ (1,2,3,4) ta được :
pM = 19 và pX = 8

Đáp án D.
Tổng số các loại hạt proton, nơtron và electron của ion M3+ là 79
p + n + e -3 = 79 => 2p + n = 82 (1)
Số hạt mang điện nhiều hơn số hạt không mang điện là 19
p + e – 3 – n = 19 hay 2p – n = 22 (2)
Từ (1), (2) ta có p = e = 26, n =30
Cấu hình e của M: [Ar]3d64s2
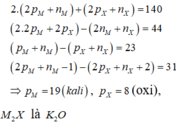


Gọi số p,e,n trong của M và X lần lượt là p1,e1,n1 , p2,e2,n2
=> 2(p1+e1+n1) + ( p2+e2+n2)=140
Mà số p=số e
=> 2(2p1 + n1) + ( 2p2 + n2) = 140 <=> (4p1+2p2) + (2n1+n2)=140 (I)
Lại có : (4p1+2p2)-(2n1+n2)=44 (II)
Từ (I) và (II ) => \(\left\{{}\begin{matrix}4p1+2p2=92\left(1\right)\\2n1+n2=48\end{matrix}\right.\)
Lại có : (p1 + n1) - (p2+n2)=23 (III)
(2p1 + n1 -1) - (2p2+n2+2) =31 (IV)
Từ (III) và (IV) => \(\left\{{}\begin{matrix}p1-p2=11\left(2\right)\\n1-n2=12\end{matrix}\right.\)
Từ (1) và (2) => \(\left\{{}\begin{matrix}p1=19\\p2=8\end{matrix}\right.\)
=> số e của M là 19 e
số e của X là 8 e
=> cấu hình e của M là : 1s22s22p63s23p64s1
cấu hình e của X là : 1s22s22p4