Cho tam giác MNP vuông tại M (MN-MP), đường cao MH. Gọi D và E lần lượt là hình chiếu của H trên MN và MP. 2/ Chứng minh: MD.MN =ME, MP MN² b/ Chứng minh: MP4 PH và chứng minh MH = NPNDPE NH có Qua M kẻ đường vuông góc với DE cắt NP tại K. Chứng minh Kỉ là trung điểm Nh d/ Cho góc P=a; NP = a. Từ M kẻ đường vuông góc với MK cắt tia PN tại I. Chứng minh PI a.(cos 2a+1) 2cos 2a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔMNP vuông tại M có MH là đường cao
nên \(NH\cdot PH=MH^2\left(1\right)\)
Xét ΔNHM vuông tại H có HE là đường cao
nên \(ME\cdot MN=MH^2\left(2\right)\)
Từ (1) và (2) suy ra \(NH\cdot PH=ME\cdot MN\)
b: Xét ΔMNP vuông tại M có MH là đường cao
nên \(\left\{{}\begin{matrix}MP^2=PH\cdot PN\\NM^2=NH\cdot NP\end{matrix}\right.\)
=>\(\dfrac{PH\cdot PN}{NH\cdot NP}=\dfrac{MP^2}{MN^2}\)
=>\(\dfrac{NH}{PH}=\left(\dfrac{MN}{MP}\right)^2\)
c: ΔMHP vuông tại H có HF là đường cao
nên \(MF\cdot MP=MH^2\)
mà \(ME\cdot MN=MH^2\)
nên \(MF\cdot MP=ME\cdot MN\)
=>\(\dfrac{MF}{ME}=\dfrac{MN}{MP}\)
Xét ΔMFN vuông tại M và ΔMEP vuông tại M có
\(\dfrac{MF}{ME}=\dfrac{MN}{MP}\)
Do đó: ΔMFN đồng dạng với ΔMEP
=>\(\widehat{MNF}=\widehat{MPE}\)

a: Xét ΔHNM vuông tại H và ΔMNP vuôg tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: NP=căn 3^2+4^2=5cm
MH=3*4/5=2,4cm
NH=3^2/5=1,8cm
c; Đề bài yêu cầu gì?

a: Xét tứ giác MDHE có
\(\widehat{MDH}=\widehat{MEH}=\widehat{EMD}=90^0\)
=>MDHE là hình chữ nhật
b: MDHE là hình chữ nhật
=>MH cắt DE tại trung điểm của mỗi đường
mà O là trung điểm của MH
nên O là trung điểm của DE
=>DO=OE
c: ΔHDN vuông tại D
mà DI là đường trung tuyến
nên DI=HI=IN
=>ΔIHD cân tại I
ΔPEH vuông tại E
mà EK là đường trung tuyến
nên EK=KP=KH
=>ΔKEH cân tại K
\(\widehat{KED}=\widehat{KEH}+\widehat{DEH}\)
\(=\widehat{KHE}+\widehat{HMD}\)
\(=\widehat{HMD}+\widehat{HND}=90^0\)
=>KE vuông góc ED(1)
\(\widehat{IDE}=\widehat{IDH}+\widehat{EDH}\)
\(=\widehat{IHD}+\widehat{EMH}\)
\(=\widehat{HPM}+\widehat{HMP}=90^0\)
=>ID vuông góc DE(2)
Từ (1) và (2) suy ra DI//EK

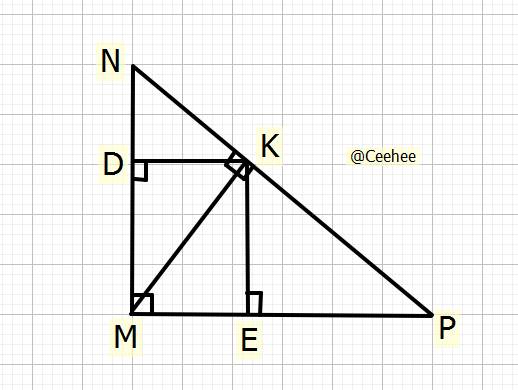
`a)` Biết `MN=7cm;NP=25cm`
Xét \(\Delta MNP\) vuông tại `M`, đường cao `MK`
Ta có: \(NP^2=MN^2+MP^2\) (đl Pytago)
\(\Rightarrow25^2=7^2+MP^2\\ \Rightarrow MP^2=25^2-7^2=576\\ \Rightarrow MP=\sqrt{576}=24cm\)
Ta có: \(\dfrac{1}{MK^2}=\dfrac{1}{MN^2}+\dfrac{1}{MP^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{MK^2}=\dfrac{1}{7^2}+\dfrac{1}{24^2}\\ \Rightarrow\dfrac{1}{MK^2}=\dfrac{625}{28224}\\ \Rightarrow MK^2=\dfrac{1\cdot28224}{625}\\ \Rightarrow MK=\sqrt{\dfrac{28224}{625}}\\ \Rightarrow MK=6,72cm\)
Ta có: \(MN^2=NK\cdot NP\left(htl\right)\)
\(\Rightarrow7^2=NK\cdot25\\ \Rightarrow NK=\dfrac{7^2}{25}=1,96cm\)
Vậy: \(MP=24cm;MK=6,72cm;NK=1,96cm\)
`b)` \(C/m:MD\cdot MN=ME\cdot MP\)
Xét \(\Delta KMN\) vuông tại `K`
Ta có: \(MK^2=MD\cdot MN\left(htl\right)\left(1\right)\)
Xét \(\Delta KMP\) vuông tại `K`
Ta có: \(MK^2=ME\cdot MP\left(htl\right)\left(2\right)\)
Từ `(1)` và `(2)` \(\Rightarrow MK^2=MK^2\)
\(\Rightarrow MD\cdot MN=ME\cdot MP\left(=MK^2\right)\)
(Câu `c)` tớ chịu :v).

Phần a,b nha
a)Xét tứ giác MDHE, có:
MDHˆ=900MDH^=900
Mˆ=900M^=900
HEMˆ=900HEM^=900
=> Tứ giác MDHE là hình chữ nhật
b) Gọi giao điểm của MH là DE là O MDHE là hình chữ nhật nên hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường
=> OH=OE
Xét tam giác EOH, có:
OH=OE(CMT)
=> Tam giác EOH cân tại O
=> H1ˆ=E1ˆH1^=E1^
Xét DEHP vuông tại E ,có:
A là trung điểm PH
=> AE = AH.
=> H2ˆ=E2ˆH2^=E2^
=> AEOˆ=AHOˆAEO^=AHO^ =900=900
Từ đó góc AEO = 900
hay tam giác DEA vuông tại E.

a: Xét tứ giác MDHE có
\(\widehat{MDH}=\widehat{MEH}=\widehat{EMD}=90^0\)
Do đó: MDHE là hình chữ nhật

2: Áp dụng hệ thức lượng trong tam giác vuông vào ΔMHN vuông tại H có HD là đường cao ứng với cạnh huyền MN, ta được:
\(MD\cdot MN=MH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔMHP vuông tại H có HE là đường cao ứng với cạnh huyền MP, ta được:
\(ME\cdot MP=MH^2\left(2\right)\)
Từ (1) và (2) suy ra \(MD\cdot MN=ME\cdot MP\)