\(\text{Cho bất phương trình :}-4\sqrt{-x^2+2x+15} \ge x^2-2x-13+m.\text{ Tìm m để bất phương trình nghiệm đúng với mọi x \in[-3;5]}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LL
1
21 tháng 8 2019
Ta có:
\(m^2-4m+3=m^2-4m+4-1=\left(m-2\right)^2-1=\left(m-3\right)\left(m-1\right)\)
\(m-m^2=m\left(1-m\right)\)
Bất phương trình <=> \(\left(m-3\right)\left(m-1\right)x+m\left(1-m\right)< 0\)
+) TH1: \(\left(m-3\right)\left(m-1\right)< 0\)
khi đó: \(x>\frac{m}{m-3}\)(loại)
+) TH2: \(\left(m-3\right)\left(m-1\right)>0\)
khi đó: \(x< \frac{m}{m-3}\)(loại)
+) Th3: \(\left(m-3\right)\left(m-1\right)=0\Leftrightarrow\orbr{\begin{cases}m=1\\m=3\end{cases}}\)
Với m=1 ta có: 0x+0<0 vô lí
Với m=3 ta có: \(0x-6< 0\)đúng với mọi x ( thỏa mãn)
Vậy m=3
CM
22 tháng 5 2018
* Nếu m= 0 thì bất phương trình đã cho trở thành:
0x < 0( luôn đúng với mọi x).
* Nếu m= 1 thì bất phương trình đã cho trở thành:
0x < 1 ( luôn đúng với mọi x)
Tập tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x là {0; 1}
CM
8 tháng 11 2018
+ Khi m = 0, bất phương trình trở thành - 2 x + 2 < 0 ⇔ x > 1 . Vậy m = 0 không thỏa mãn yêu cầu của bài toán.
+ Khi m ≠ 0 , bất phương trình vô nghiệm khi m x 2 + 2 m - 1 x + m + 2 ≥ 0 , ∀ x ∈ ℝ . ⇔ a > 0 ∆ ' ≤ 0 ⇔ m > 0 ( m - 1 ) 2 - m ( m + 2 ) ≤ 0 .
⇔ m > 0 - 4 m + 1 ≤ 0 ⇔ m > 0 m ≥ 1 4 ⇔ m ≥ 1 4
Chọn C.
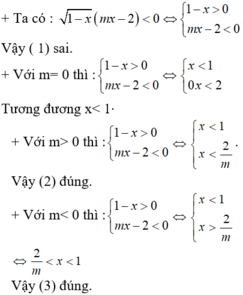
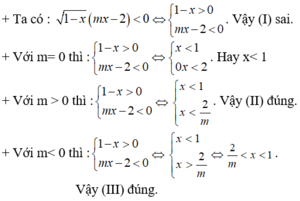
Đặt \(\sqrt{-x^2+2x+15}=t\Rightarrow0\le t\le4\)
BPT trở thành:
\(-4t\ge-t^2+2+m\)
\(\Leftrightarrow t^2-4t-2\ge m\)
\(\Rightarrow m\le\min\limits_{\left[0;4\right]}\left(t^2-4t-2\right)\)
Xét \(f\left(t\right)=t^2-4t-2\) trên \(\left[0;4\right]\)
\(-\dfrac{b}{2a}=2\in\left[0;4\right]\)
\(f\left(0\right)=f\left(4\right)=-2\) ; \(f\left(2\right)=-6\)
\(\Rightarrow f\left(t\right)_{min}=-6\Rightarrow m\le-6\)